题目内容
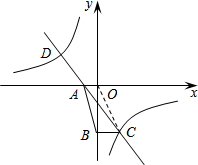 如图,直线y=kx+k(k≠0)与双曲线y=
如图,直线y=kx+k(k≠0)与双曲线y=| n |
| x |
(1)求点A的坐标;
(2)过点C作CB⊥y轴,垂足为B,若S△ABC=4,求双曲线的解析式;
(3)在(1)(2)的条件下,若AB=
| 17 |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)在直线y=kx+k中令y=0可求得A点坐标;
(2)连接OC,根据条件可知S△ABC=S△OBC=
|n|,可求得n,可得到双曲线的解析式;
(3)可设B点坐标,根据条件可先求得B点坐标,则可得到C点纵坐标,代入双曲线可求得C点坐标,把C点坐标代入直线可求得直线解析式,联立两解析式可求得D点坐标.
(2)连接OC,根据条件可知S△ABC=S△OBC=
| 1 |
| 2 |
(3)可设B点坐标,根据条件可先求得B点坐标,则可得到C点纵坐标,代入双曲线可求得C点坐标,把C点坐标代入直线可求得直线解析式,联立两解析式可求得D点坐标.
解答:解:(1)在y=kx+k中,令y=0可得0=kx+k,解得x=-1,
∴A点坐标为(-1,0);
(2)如图,连接OC,
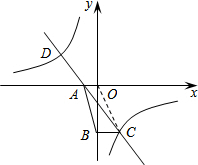
则S△ABC=S△OBC=
|n|=4,
∵n<0,
∴n=-8,
∴双曲线解析式为y=-
;
(3)设B点坐标为(0,b)(b<0),
则OB=|b|,又OA=1,
在Rt△AOB中,由勾股定理可得OA2+OB2=AB2,
∴1+b2=17,解得b=-4,
∴C点纵坐标为-4,代入双曲线解析式可得-4=-
,解得x=2,
∴C点坐标为(2,-4),
把C点坐标代入直线y=kx+k可得-4=2k+k,解得k=-
,
∴直线解析式为y=-
x-
,
联立直线和双曲线解析式可得
,解得
(舍去),
,
∴D点坐标为(-3,
).
∴A点坐标为(-1,0);
(2)如图,连接OC,

则S△ABC=S△OBC=
| 1 |
| 2 |
∵n<0,
∴n=-8,
∴双曲线解析式为y=-
| 8 |
| x |
(3)设B点坐标为(0,b)(b<0),
则OB=|b|,又OA=1,
在Rt△AOB中,由勾股定理可得OA2+OB2=AB2,
∴1+b2=17,解得b=-4,
∴C点纵坐标为-4,代入双曲线解析式可得-4=-
| 8 |
| x |
∴C点坐标为(2,-4),
把C点坐标代入直线y=kx+k可得-4=2k+k,解得k=-
| 4 |
| 3 |
∴直线解析式为y=-
| 4 |
| 3 |
| 4 |
| 3 |
联立直线和双曲线解析式可得
|
|
|
∴D点坐标为(-3,
| 8 |
| 3 |
点评:本题主要考查待定系数法求函数解析式及函数图象的交点,掌握两函数图象的交点坐标满足两函数解析式是解题的关键,注意反比例函数y=
中k的几何意义的应用.
| k |
| x |

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
在直角坐标平面中,M(2,0),圆M的半径为4,那么点P(-2,3)与圆M的位置关系是( )
| A、点P在圆内 | B、点P在圆上 |
| C、点P在圆外 | D、不能确定 |
下列运算正确的是( )
| A、2m3+m3=3m6 | ||
| B、m3•m2=m6 | ||
| C、(-m4)3=m7 | ||
D、m6÷2m2=
|
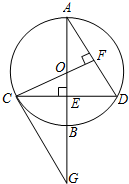 如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,
如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G, 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,CD=4,cosA=
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,CD=4,cosA=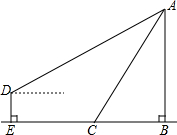 如图,小明想测量河对岸的一幢高楼AB蛾高度,小明在河边C处测得楼顶A的仰角是60°距C处60米的E处有幢楼房,小明从该楼房中距地面20米的D处测得楼顶A的仰角是30°(点B、C、E在同一直线上,且AB、DE均与地面BE处置),求楼AB的高度.
如图,小明想测量河对岸的一幢高楼AB蛾高度,小明在河边C处测得楼顶A的仰角是60°距C处60米的E处有幢楼房,小明从该楼房中距地面20米的D处测得楼顶A的仰角是30°(点B、C、E在同一直线上,且AB、DE均与地面BE处置),求楼AB的高度.