题目内容
已知一次函数y=kx+2(k≠0)图象过点(3,-4),求不等式kx+2≤0的解集.
考点:一次函数与一元一次不等式
专题:计算题
分析:先根据一次函数图象上点的坐标特征得到3k+2=-4,解得k=-2,然后解不等式-2x+2≤0即可.
解答:解:∵一次函数y=kx+2(k≠0)图象过点(3,-4),
∴3k+2=-4,解得k=-2,
∴一次函数解析式为y=-2x+2,
解不等式-2x+2≤0得x≥1,
即不等式kx+2≤0的解集为x≥1.
∴3k+2=-4,解得k=-2,
∴一次函数解析式为y=-2x+2,
解不等式-2x+2≤0得x≥1,
即不等式kx+2≤0的解集为x≥1.
点评:本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
用一个2倍放大镜照一个△ABC,下面说法中错误的是( )
| A、△ABC放大后,是原来的2倍 |
| B、△ABC放大后,各边长是原来的2倍 |
| C、△ABC放大后,周长是原来的2倍 |
| D、△ABC放大后,面积是原来的4倍 |
在直角坐标平面中,M(2,0),圆M的半径为4,那么点P(-2,3)与圆M的位置关系是( )
| A、点P在圆内 | B、点P在圆上 |
| C、点P在圆外 | D、不能确定 |
 如图,抛物线y=-x2-4x+5交坐标轴于A、B、C三点,点P在第二象限的抛物线上,PF⊥x轴于F点,交AC于E点.若S△PAE:S△AEF=2:3,求P点坐标.
如图,抛物线y=-x2-4x+5交坐标轴于A、B、C三点,点P在第二象限的抛物线上,PF⊥x轴于F点,交AC于E点.若S△PAE:S△AEF=2:3,求P点坐标.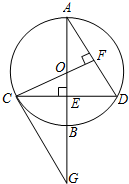 如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,
如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G, 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题: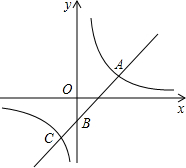 如图,在平面直角坐标系xOy中,反比例函数y=
如图,在平面直角坐标系xOy中,反比例函数y=