题目内容
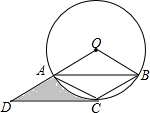 如图,⊙O是△ABC的外接圆,AC=BC,CD∥AB交OA的延长线于点D.
如图,⊙O是△ABC的外接圆,AC=BC,CD∥AB交OA的延长线于点D.(1)求证:DC是⊙O的切线;
(2)若∠ABC=30°,求证:四边形AOBC是菱形;
(3)若∠ABC=30°,OA=1,求DC的长及AD、DC及弧AC围成的图形的面积.
考点:切线的判定,菱形的判定,扇形面积的计算
专题:
分析:(1)根据线段垂直平分线性质求出OC⊥AB,推出OC⊥CD,根据切线的判定推出即可;
(2)求出∠AOB=120°,求出∠OAB=∠OBA=∠CAB=∠ABC,推出OA∥BC,OB∥AC,得出平行四边形AOBC,根据菱形的判定推出即可;
(3)求出AB长,即可求出DC长,求出∠AOC的度数,分别求出三角形DCO和扇形AOC的面积,即可得出答案.
(2)求出∠AOB=120°,求出∠OAB=∠OBA=∠CAB=∠ABC,推出OA∥BC,OB∥AC,得出平行四边形AOBC,根据菱形的判定推出即可;
(3)求出AB长,即可求出DC长,求出∠AOC的度数,分别求出三角形DCO和扇形AOC的面积,即可得出答案.
解答:(1)证明:如图1,连接OC交AB于E,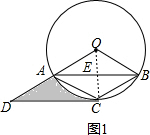
∵AC=BC,OA=OB,
∴OC垂直平分AB,
即AE=BE,OC⊥AB,
∵DC∥AB,
∴OC⊥DC,
∵OC为半径,
∴DC是⊙O的切线;
(2)证明:如图2,作圆周角AMB,则∠AMB=
∠AOB,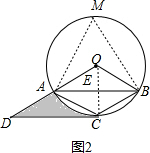
∵AC=BC,∠ABC=30°,
∴∠CAB=∠ABC=30°,∠ACB=180°-30°-30°=120°,
则∠AMB=180°-120°=60°,
∴∠AOB=2∠AMB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∴∠OBA=∠CAB,∠OAB=∠ABC,
∴OA∥BC,OB∥AC,
∵OA=OB,
∴四边形AOBC是菱形;
(3)解:∵OC⊥AB,∠OAB=30°,OA=1,
∴OE=
OA=
,由勾股定理得:AE=
=
,∠AOC=90°-30°=60°,
∴AB=2AE=
,
∵四边形AOBC是菱形,
∴OA∥BC,
∵DC∥AB,
∴四边形ABCD是平行四边形,
∴DC=AB=
,AD=BC=AO=1,
∴阴影部分的面积S=S△DCO-S扇形AOC=
×
×1-
=
-
π.

∵AC=BC,OA=OB,
∴OC垂直平分AB,
即AE=BE,OC⊥AB,
∵DC∥AB,
∴OC⊥DC,
∵OC为半径,
∴DC是⊙O的切线;
(2)证明:如图2,作圆周角AMB,则∠AMB=
| 1 |
| 2 |

∵AC=BC,∠ABC=30°,
∴∠CAB=∠ABC=30°,∠ACB=180°-30°-30°=120°,
则∠AMB=180°-120°=60°,
∴∠AOB=2∠AMB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∴∠OBA=∠CAB,∠OAB=∠ABC,
∴OA∥BC,OB∥AC,
∵OA=OB,
∴四边形AOBC是菱形;
(3)解:∵OC⊥AB,∠OAB=30°,OA=1,
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
| OA2-OE2 |
| ||
| 2 |
∴AB=2AE=
| 3 |
∵四边形AOBC是菱形,
∴OA∥BC,
∵DC∥AB,
∴四边形ABCD是平行四边形,
∴DC=AB=
| 3 |
∴阴影部分的面积S=S△DCO-S扇形AOC=
| 1 |
| 2 |
| 3 |
| 60π×12 |
| 360 |
| ||
| 2 |
| 1 |
| 6 |
点评:本题考查了扇形的面积,三角形的面积,切线的判定,垂径定理,线段垂直平分线性质,勾股定理,含30度角的直角三角形的性质,平行四边形的判定和性质等知识点的应用,能正确作出辅助线并能综合运用性质进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线y=-x2+x-1与坐标轴(含x轴、y轴)的公共点的个数是( )
| A、0 | B、1 | C、2 | D、3 |
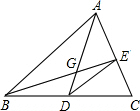 如图,已知AD是△ABC的中线,G是△ABC的重心,联结BG并延长交AC于点E,联结DE,则S△ABC:S△CED的值为
如图,已知AD是△ABC的中线,G是△ABC的重心,联结BG并延长交AC于点E,联结DE,则S△ABC:S△CED的值为 如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD;
如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD;
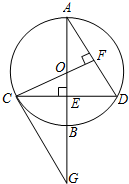 如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,
如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,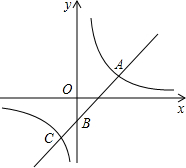 如图,在平面直角坐标系xOy中,反比例函数y=
如图,在平面直角坐标系xOy中,反比例函数y=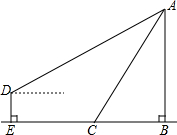 如图,小明想测量河对岸的一幢高楼AB蛾高度,小明在河边C处测得楼顶A的仰角是60°距C处60米的E处有幢楼房,小明从该楼房中距地面20米的D处测得楼顶A的仰角是30°(点B、C、E在同一直线上,且AB、DE均与地面BE处置),求楼AB的高度.
如图,小明想测量河对岸的一幢高楼AB蛾高度,小明在河边C处测得楼顶A的仰角是60°距C处60米的E处有幢楼房,小明从该楼房中距地面20米的D处测得楼顶A的仰角是30°(点B、C、E在同一直线上,且AB、DE均与地面BE处置),求楼AB的高度.