题目内容
4．解方程：$\frac{2x+5}{x+2}-\frac{1}{2x+4}$=1．分析 方程两边都乘以2（x+2）得到2（2x+5）-1=2x+4，解得x=-$\frac{5}{2}$，然后进行检验确定分式方程的解．
解答 解：$\frac{2x+5}{x+2}-\frac{1}{2x+4}$=1，
去分母，得2（2x+5）-1=2x+4，
去括号，得4x+10-1=2x+4，
移项，合并同类项得2x=-5，
系数化为1，得$x=-\frac{5}{2}$，
经检验，$x=-\frac{5}{2}$是原方程的解．
点评 本题考查了解分式方程：先去分母，把分式方程转化为整式方程，再解整式方程，然后把整式方程的解代入分式方程进行检验，最后确定分式方程的解．
练习册系列答案
出彩同步大试卷系列答案
相关题目
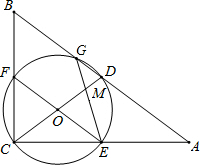如图，在△ABC中，∠ACB=90°，D是AB的中点，以DC为直径的⊙O交△ABC的三边，交点分别是G、F、E点，GE，CD的交点为M，且ME=4$\sqrt{6}$，MD：CO=2：5．
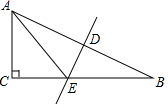如图，在Rt△ABC中，∠C=90°，AB边的垂直平分线DE交BC于点E，垂足为D．
如图，方格图中每个小正方形的边长为1，点A、B、C都是格点．