题目内容
9.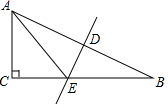 如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.
如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.
分析 根据线段垂直平分线的性质得出AE=BE,再由直角三角形的性质即可得出结论.
解答 证明:∵DE是AB的垂直平分线,
∴EA=EB.
∴∠EAB=∠B.
∵∠C=90°,
∴∠CAB+∠B=90°.
又∵∠AED+∠EAB=90°,
∴∠CAB=∠AED.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
17.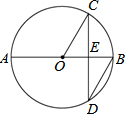 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )| A. | 6 | B. | 5 | C. | 3$\sqrt{3}$ | D. | 3 |
14.把抛物线y=-x2向右平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
| A. | y=-(x-1)2-3 | B. | y=-(x+1)2-3 | C. | y=-(x-1)2+3 | D. | y=-(x+1)2+3 |
1.一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( )
| A. | 120° | B. | 130° | C. | 135° | D. | 150° |
18.下列各式由左到右的变形中,属于分解因式的是( )
| A. | a(m+n)=am+an | B. | a2-b2-c2=(a-b)(a+b)-c2 | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+6x=(x+4)(x-4)+6x |
19. 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )
 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )| A. | 100分 | B. | 80分 | C. | 60分 | D. | 40分 |
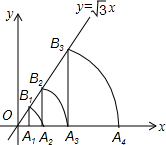 如图,直线y=$\sqrt{3}$x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点A6的坐标为(32,0).
如图,直线y=$\sqrt{3}$x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点A6的坐标为(32,0).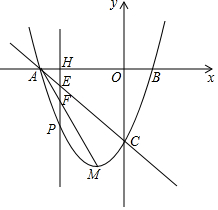 在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.