题目内容
14.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=$\frac{12}{5}$或$\frac{5}{3}$时,以A、D、E为顶点的三角形与△ABC相似.分析 若A,D,E为顶点的三角形与△ABC相似时,则$\frac{AE}{AD}$=$\frac{AB}{AC}$或$\frac{AD}{AE}$=$\frac{AB}{AC}$,分情况进行讨论后即可求出AE的长度.
解答 解:当$\frac{AE}{AD}$=$\frac{AB}{AC}$时,
∵∠A=∠A,
∴△AED∽△ABC,
此时AE=$\frac{AB•AD}{AC}$=$\frac{6×2}{5}$=$\frac{12}{5}$;
当$\frac{AD}{AE}$=$\frac{AB}{AC}$时,
∵∠A=∠A,
∴△ADE∽△ABC,
此时AE=$\frac{AC•AD}{AB}$=$\frac{5×2}{6}$=$\frac{5}{3}$;
故答案为:$\frac{12}{5}$或$\frac{5}{3}$.
点评 本题考查了相似三角形的判定,熟练掌握相似三角形的判定方法,解题的关键是分两种情况进行讨论.

练习册系列答案
相关题目
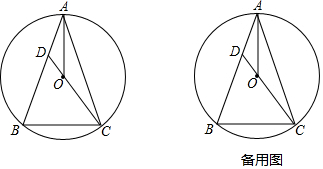
19. 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )
 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )| A. | 100分 | B. | 80分 | C. | 60分 | D. | 40分 |
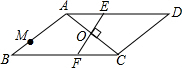 如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.
如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.


 如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )
如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )



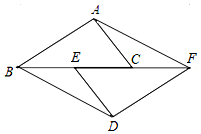 如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.