题目内容
12.若A(x1,y1),B(x2,y2),C(x3,y3)是双曲线y=$\frac{2}{x}$上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是y1<y3<y2.分析 先根据反比例函数y=$\frac{2}{x}$的系数2>0判断出函数图象在一、三象限,在每个象限内,y随x的增大而减小,再根据x1<0<x2<x3,判断出y1、y2、y3的大小.
解答 解:∵k>0,
∴函数图象如图,则图象在第一、三象限,在每个象限内,y随x的增大而减小,
又∵x1<0<x2<x3,
∴y1<y3<y2.
故答案是:y1<y3<y2.
点评 本题考查了由反比例函数的图象和性质确定y2,y1,y3的关系.注意是在每个象限内,y随x的增大而减小.不能直接根据x的大小关系确定y的大小关系.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
17.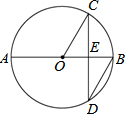 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )| A. | 6 | B. | 5 | C. | 3$\sqrt{3}$ | D. | 3 |
1.一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( )
| A. | 120° | B. | 130° | C. | 135° | D. | 150° |
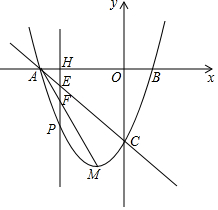 在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C. 国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.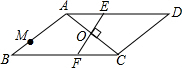 如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.
如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.