题目内容
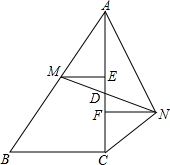 如图,AB=10,AC=8,BC=6,M是AB的中点,点D在线段AC上,且D是MN的中点,ME⊥AC于点E,NF⊥AC于点F.设AD=x,DM=y.
如图,AB=10,AC=8,BC=6,M是AB的中点,点D在线段AC上,且D是MN的中点,ME⊥AC于点E,NF⊥AC于点F.设AD=x,DM=y.(1)求NF;
(2)确定x与y的数量关系;
(3)若⊙N的半径为AN,那么x分别取何值时,⊙N与直线AC、AB、BC相切.
考点:圆的综合题
专题:
分析:(1)先由勾股定理的逆定理得到∠ACB=90°,进而得ME∥BC,求得ME=
BC=3,再根据ME∥FN即可求得NF的长;
(2)先用x表示出ED,再在在Rt△MED中,由勾股定理即可得答案;
(3)延长MA到P,使MA=AP;连接MC,并延长到Q,使MC=CQ;连接PQ,则不论x取何值,点N总在PQ上.再分三种情况讨论即可.
| 1 |
| 2 |
(2)先用x表示出ED,再在在Rt△MED中,由勾股定理即可得答案;
(3)延长MA到P,使MA=AP;连接MC,并延长到Q,使MC=CQ;连接PQ,则不论x取何值,点N总在PQ上.再分三种情况讨论即可.
解答:解:(1)∵AC2+BC2=82+62=100,AB2=102=100;
∴AB2=AC2+BC2.
∴∠ACB=90°.
∵ME⊥AC于点E,
∴∠AEM=∠ACB=90°.
∴ME∥BC.
∵M是AB的中点,
∴ME=
BC=3.
∵D是MN的中点,
∴MD=ND.
∵NF⊥AC于点F,
∴ME∥FN.
∴
=
.
∴NF=ME=3;
(2)∵ME∥BC,M是AB的中点,
∴AE=EC=
AC=4.
∴ED=x-4.
∴在Rt△MED中,由勾股定理得,
DM2=ME2+DE2,
即y2=32+(x-4)2,
y2=x2-8x+25;
(3)延长MA到P,使MA=AP;
连接MC,并延长到Q,使MC=CQ;
连接PQ,则不论x取何值,点N总在PQ上.
①作AN1⊥AC,如图1交PQ于点N1,
则⊙N1与AC相切于点A.
设MN1与AC交于点D1,x=
AE=
×4,此时,x=2.
②作AN2⊥AB,如图2,交PQ于点N2,
则⊙N2与AB相切于点A.
设MN2与AC交于点D2,则有32+(4-x)2=x2,
解得x=
.
③取点N3,如图3,使N3到BC的距离等于A N3,
则⊙N3与BC相切.设MN3与AC交于
点D3,则有32+(2x-4)2=(12-2x)2
解得x=
.

∴AB2=AC2+BC2.
∴∠ACB=90°.
∵ME⊥AC于点E,
∴∠AEM=∠ACB=90°.
∴ME∥BC.
∵M是AB的中点,
∴ME=
| 1 |
| 2 |
∵D是MN的中点,
∴MD=ND.
∵NF⊥AC于点F,
∴ME∥FN.
∴
| FN |
| ME |
| ND |
| MD |
∴NF=ME=3;
(2)∵ME∥BC,M是AB的中点,
∴AE=EC=
| 1 |
| 2 |
∴ED=x-4.
∴在Rt△MED中,由勾股定理得,
DM2=ME2+DE2,
即y2=32+(x-4)2,
y2=x2-8x+25;
(3)延长MA到P,使MA=AP;
连接MC,并延长到Q,使MC=CQ;
连接PQ,则不论x取何值,点N总在PQ上.
①作AN1⊥AC,如图1交PQ于点N1,
则⊙N1与AC相切于点A.
设MN1与AC交于点D1,x=
| 1 |
| 2 |
| 1 |
| 2 |
②作AN2⊥AB,如图2,交PQ于点N2,
则⊙N2与AB相切于点A.
设MN2与AC交于点D2,则有32+(4-x)2=x2,
解得x=
| 25 |
| 8 |
③取点N3,如图3,使N3到BC的距离等于A N3,
则⊙N3与BC相切.设MN3与AC交于
点D3,则有32+(2x-4)2=(12-2x)2
解得x=
| 119 |
| 32 |

点评:本题主要考查了圆的切线的性质、勾股定理、平行线分线段成比例定理等,综合性较强.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )| A、150° | B、130° |
| C、120° | D、100° |
 如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程x2-7x+12=0的两根.
如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程x2-7x+12=0的两根. 如图,在正方形ABCD中,E为AB的中点,AF垂直DE于点O,
如图,在正方形ABCD中,E为AB的中点,AF垂直DE于点O,