题目内容
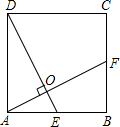 如图,在正方形ABCD中,E为AB的中点,AF垂直DE于点O,
如图,在正方形ABCD中,E为AB的中点,AF垂直DE于点O,(1)证明:点F是BC的中点;
(2)求OA:OF的值.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质可得AB=AD,再根据同角的余角相等求出∠1=∠2,然后利用“角边角”证明△ABF和△DAE全等,根据全等三角形对应边相等可得BF=AE,从而得证;
(2)设正方形的边长为2a,利用勾股定理列式求出DE,再利用三角形的面积列式求出AO,然后表示出OF,再相比即可.
(2)设正方形的边长为2a,利用勾股定理列式求出DE,再利用三角形的面积列式求出AO,然后表示出OF,再相比即可.
解答: (1)证明:在正方形ABCD中,AB=AD,∠1+∠3=90°,
(1)证明:在正方形ABCD中,AB=AD,∠1+∠3=90°,
∵AF⊥DE,
∴∠2+∠3=90°,
∴∠1=∠2,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(ASA),
∴BF=AE,
∵E为AB的中点,
∴AE=
AB,
∴BF=
BC,
∴点F是BC的中点;
(2)解:设正方形的边长为2a,
则AE=
AB=a,
由勾股定理得,DE=
=
=
a,
S△ADE=
×2a×a=
×
a•OA,
解得OA=
a,
∴OF=AF-OA=
a-
a=
a,
∴OA:OF=
a:
a=2:3.
 (1)证明:在正方形ABCD中,AB=AD,∠1+∠3=90°,
(1)证明:在正方形ABCD中,AB=AD,∠1+∠3=90°,∵AF⊥DE,
∴∠2+∠3=90°,
∴∠1=∠2,
在△ABF和△DAE中,
|
∴△ABF≌△DAE(ASA),
∴BF=AE,
∵E为AB的中点,
∴AE=
| 1 |
| 2 |
∴BF=
| 1 |
| 2 |
∴点F是BC的中点;
(2)解:设正方形的边长为2a,
则AE=
| 1 |
| 2 |
由勾股定理得,DE=
| AD2+AE2 |
| (2a)2+a2 |
| 5 |
S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
解得OA=
2
| ||
| 5 |
∴OF=AF-OA=
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
∴OA:OF=
2
| ||
| 5 |
3
| ||
| 5 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,熟记性质并确定出三角形全等的条件是解题的关键,(2)设正方形的边长然后分别表示出OA、OF计算更简便.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
(-3)m+3•(-3)m-1的值是( )
| A、1 |
| B、-1 |
| C、0 |
| D、(-3)m+1 |
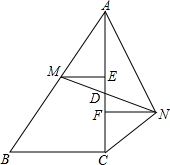 如图,AB=10,AC=8,BC=6,M是AB的中点,点D在线段AC上,且D是MN的中点,ME⊥AC于点E,NF⊥AC于点F.设AD=x,DM=y.
如图,AB=10,AC=8,BC=6,M是AB的中点,点D在线段AC上,且D是MN的中点,ME⊥AC于点E,NF⊥AC于点F.设AD=x,DM=y.