题目内容
 如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程x2-7x+12=0的两根.
如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程x2-7x+12=0的两根.(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请
| 直 |
| • |
| 接 |
| • |
考点:一次函数综合题
专题:
分析:(1)首先解方程,求得OA、OB的长度,即求得A、B的坐标,利用待定系数法即可求解;
(2)分P在B点的上边和在B的下边两种情况进行讨论,求得Q的坐标.
(2)分P在B点的上边和在B的下边两种情况进行讨论,求得Q的坐标.
解答:解:(1)∵x2-7x+12=0,
∴(x-3)(x-4)=0,
∴x=3,x=4.
∴点A的坐标为(3,0),点B的坐标为(0,4).
∵设直线AB的函数表达式为y=kx+b(k≠0)
∴
∴
∴直线AB的函数表达式为y=-
x+4.
(2)当P在B的下边时,AB是菱形的对角线,AB的中点D坐标是(
,2),
设过D点,与直线AB垂直的直线的解析式是y=
x+m,则
+m=2,
解得:m=
,
则P的坐标是(0,
).
设Q的坐标是(x,y),则
=
,
=2,
解得:x=3,y=
,
则Q点的坐标是:(3,
).
当P在B点的上方时,AB=
=5,
AQ=5,则Q点的坐标是(3,5).
总之,Q点的坐标是(3,5)或(3,
).
∴(x-3)(x-4)=0,
∴x=3,x=4.
∴点A的坐标为(3,0),点B的坐标为(0,4).
∵设直线AB的函数表达式为y=kx+b(k≠0)
∴
|
∴
|
∴直线AB的函数表达式为y=-
| 4 |
| 3 |
(2)当P在B的下边时,AB是菱形的对角线,AB的中点D坐标是(
| 3 |
| 2 |
设过D点,与直线AB垂直的直线的解析式是y=
| 3 |
| 4 |
| 9 |
| 8 |
解得:m=
| 7 |
| 8 |
则P的坐标是(0,
| 7 |
| 8 |
设Q的坐标是(x,y),则
| x |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
解得:x=3,y=
| 25 |
| 8 |
则Q点的坐标是:(3,
| 25 |
| 8 |
当P在B点的上方时,AB=
| 32+42 |
AQ=5,则Q点的坐标是(3,5).
总之,Q点的坐标是(3,5)或(3,
| 25 |
| 8 |
点评:本题考查了待定系数法求函数的解析式,以及菱形的性质,正确对P的位置进行分类讨论是关键.

练习册系列答案
相关题目
满足不等式组
的整数解个数有( )
|
| A、4个 | B、3个 | C、2个 | D、1个 |
(-3)m+3•(-3)m-1的值是( )
| A、1 |
| B、-1 |
| C、0 |
| D、(-3)m+1 |
关于x的二次函数y=(x-m)2-1的图象与x轴交于A,B两点,与y轴交于点C.下列说法正确的是( )
| A、点C的坐标是(0,-1) |
| B、点(1,-m2)在该二次函数的图象上 |
| C、线段AB的长为2m |
| D、若当x≤1时,y随x的增大而减小,则m≥1 |
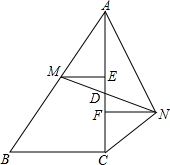 如图,AB=10,AC=8,BC=6,M是AB的中点,点D在线段AC上,且D是MN的中点,ME⊥AC于点E,NF⊥AC于点F.设AD=x,DM=y.
如图,AB=10,AC=8,BC=6,M是AB的中点,点D在线段AC上,且D是MN的中点,ME⊥AC于点E,NF⊥AC于点F.设AD=x,DM=y.