题目内容
如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（ ）| A、150° | B、130° |
| C、120° | D、100° |
考点：平行四边形的性质
专题：
分析：由在平行四边形ABCD中，∠ABC的平分线交AD于E，易证得△ABE是等腰三角形，又由∠BED=150°，即可求得∠A的大小．
解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠AEB=∠CBE，
∵BE平分∠ABE，
∴∠ABE=∠CBE，
∴∠AEB=∠ABE，
∴AB=AE，
∵∠BED=150°，
∴∠ABE=∠AEB=30°，
∴∠A=180°-∠ABE-∠AEB=120°．
故选C．
∴AD∥BC，
∴∠AEB=∠CBE，
∵BE平分∠ABE，
∴∠ABE=∠CBE，
∴∠AEB=∠ABE，
∴AB=AE，
∵∠BED=150°，
∴∠ABE=∠AEB=30°，
∴∠A=180°-∠ABE-∠AEB=120°．
故选C．
点评：此题考查了平行四边形的性质以及等腰三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
如图，?ABCD的周长为16cm，AC、BD交于点O，且AD＞CD，过O作OM⊥AC，交AD于点M，则△CDM的周长为满足不等式组
的整数解个数有（ ）
|
| A、4个 | B、3个 | C、2个 | D、1个 |
如图，△ABC中，∠A=45°，∠ABC=90°，BD⊥AC于D，则图中等腰三角形的个数是（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
若（x+m）（x-3）=x2-nx-12，则m、n的值为（ ）
| A、m=4，n=-1 |
| B、m=4，n=1 |
| C、m=-4，n=1 |
| D、m=-4，n=-1 |
已知关于x的方程x2-10x+m=0有两个相等的实数根，则m=（ ）
| A、10 | B、25 |
| C、-25 | D、±25 |
（-3）m+3•（-3）m-1的值是（ ）
| A、1 |
| B、-1 |
| C、0 |
| D、（-3）m+1 |
关于x的二次函数y=（x-m）2-1的图象与x轴交于A，B两点，与y轴交于点C．下列说法正确的是（ ）
| A、点C的坐标是（0，-1） |
| B、点（1，-m2）在该二次函数的图象上 |
| C、线段AB的长为2m |
| D、若当x≤1时，y随x的增大而减小，则m≥1 |
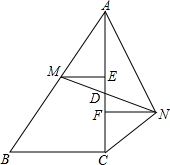如图，AB=10，AC=8，BC=6，M是AB的中点，点D在线段AC上，且D是MN的中点，ME⊥AC于点E，NF⊥AC于点F．设AD=x，DM=y．