题目内容
8.化简:$\sqrt{(x+3)^{2}}$-$\sqrt{(2-x)^{2}}$+($\sqrt{x-3}$)2.分析 根据$\sqrt{(x+3)^{2}}$-$\sqrt{(2-x)^{2}}$+($\sqrt{x-3}$)2可知x-3≥0,从而可以得到x≥3,从而可以化简所求的式子,本题得以解决.
解答 解:∵$\sqrt{(x+3)^{2}}$-$\sqrt{(2-x)^{2}}$+($\sqrt{x-3}$)2有意义,
∴x-3≥0,
∴x≥3,
∴$\sqrt{(x+3)^{2}}$-$\sqrt{(2-x)^{2}}$+($\sqrt{x-3}$)2
=x+3-(x-2)+x-3
=x+3-x+2+x-3
=x+2.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式混合运算的计算方法,发现其中的隐含条件.

练习册系列答案
相关题目
 如图,在△ABC中,∠B=∠C,点O是底边BC的中点,OD⊥AB,OE⊥AC,垂足分别为D、E,证明OD=OE.
如图,在△ABC中,∠B=∠C,点O是底边BC的中点,OD⊥AB,OE⊥AC,垂足分别为D、E,证明OD=OE.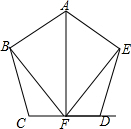 如图,点F是CD 的中点,且AF⊥CD,BC=ED,∠BCD=∠EDC.
如图,点F是CD 的中点,且AF⊥CD,BC=ED,∠BCD=∠EDC. 求证:三角形的重心将中线分成2:1.
求证:三角形的重心将中线分成2:1. 周老伯想利用一边长为12米的旧墙及24米长的篱笆围建猪舍三间,它们的平面图(如图)是一排大小相等的长方形.
周老伯想利用一边长为12米的旧墙及24米长的篱笆围建猪舍三间,它们的平面图(如图)是一排大小相等的长方形.