题目内容
18.解方程组:$\left\{\begin{array}{l}{3{x}^{2}+xy+{y}^{2}=15}\\{3{x}^{2}-31xy+5{y}^{2}=-45}\end{array}\right.$.分析 将①×3+②得x2-7xy+2y2=0,即(x-2y)(3x-y)=0,从而可得x=2y或3x=y,再分别代入方程①即可求得方程组的解.
解答 解:解方程组$\left\{\begin{array}{l}{3{x}^{2}+xy+{y}^{2}=15}&{①}\\{3{x}^{2}-31xy+5{y}^{2}=-45}&{②}\end{array}\right.$,
①×3+②,得:12x2-28xy+8y2=0,即x2-7xy+2y2=0,
左边因式分解,得:(x-2y)(3x-y)=0,
∴x=2y或3x=y,
将x=2y代入①,得:12y2+2y2+y2=15,即15y2=15,
解得:y=±1,
∴此时方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$;
将3x=y代入①,得:15x2=15,
解得:x=±1,
∴此时方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$;
综上,方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$.
点评 本题主要考查解高次方程的能力,高次方程的解法思想:通过适当的方法,把高次方程化为次数较低的方程求解.所以解高次方程一般要降次,即把它转化成二次方程或一次方程.也有的通过因式分解来解.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 86 | 100 | 98 | 119 | 97 | 500 |
| 优秀率 | 中位数 | 方差 | |
| 甲班 | 60% | 100 | 46.8 |
| 乙班 | 40% | 98 | 114 |
友情提示:一组数据的方差计算公式是S2=$\frac{1}{n}$[(x1-x)2+(x2-x)2+…+(xn-x)2],其中$\overline{x}$为n个数据x1,x2,…,xn的平均数.
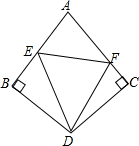 如图,BD=CD,∠ABD=∠ACD=90°,点E,F分别在AB,AC上,若ED平分∠BEF
如图,BD=CD,∠ABD=∠ACD=90°,点E,F分别在AB,AC上,若ED平分∠BEF 如图,△ABC中,BE⊥AD于点E,CF⊥AD于点F,且BE=CF,试说明BD=CD.
如图,△ABC中,BE⊥AD于点E,CF⊥AD于点F,且BE=CF,试说明BD=CD.