题目内容
4. 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D=35°.
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D=35°.
分析 根据折叠的性质求出∠EDC′,根据三角形的中位线求出DE∥AB,根据平行线的性质求出即可.
解答 解:∵将△CDE沿DE折叠,使点C落在AB边上的点C′处,∠CDE=35°,
∴∠EDC′=∠CDE=35°,
∵D、E分别为△ABC的AC,BC边的中点,
∴DE∥AB,
∴∠AC′D=∠EDC′=35°,
故答案为:35°.
点评 本题考查了三角形的中位线,折叠的性质,平行线的性质的应用,能求出∠EDC′=∠CDE和DE∥AB是解此题的关键.

练习册系列答案
相关题目
16. 为了培养学生良好的课外阅读习惯,某校2500名学生参加了“为中华崛起而读书”活动,为了了解在活动前后一周学生的阅读量(单位:h)情况,该校抽查了参加活动的其中50名学生的阅读量,并绘制了如图的统计图.
为了培养学生良好的课外阅读习惯,某校2500名学生参加了“为中华崛起而读书”活动,为了了解在活动前后一周学生的阅读量(单位:h)情况,该校抽查了参加活动的其中50名学生的阅读量,并绘制了如图的统计图.
请你根据图示信息回答下列问题:
(1)请在条形统计图的括号中标出B等级活动前后的人数.
(2)在活动开展前,这50名学生阅读量的中位数所在的等级是A.
(3)参加活动的2500名学生中,活动开展前阅读量不超过1.5h的学生大约有1300名;活动开展后阅读量超过1.5h的学生大约有2350名.
 为了培养学生良好的课外阅读习惯,某校2500名学生参加了“为中华崛起而读书”活动,为了了解在活动前后一周学生的阅读量(单位:h)情况,该校抽查了参加活动的其中50名学生的阅读量,并绘制了如图的统计图.
为了培养学生良好的课外阅读习惯,某校2500名学生参加了“为中华崛起而读书”活动,为了了解在活动前后一周学生的阅读量(单位:h)情况,该校抽查了参加活动的其中50名学生的阅读量,并绘制了如图的统计图.| 一周阅读量/h | 0.5~1.5 | 1.6~2.5 | 2.6~3.5 | 3.6~4.5 |
| 等级 | A | B | C | D |
(1)请在条形统计图的括号中标出B等级活动前后的人数.
(2)在活动开展前,这50名学生阅读量的中位数所在的等级是A.
(3)参加活动的2500名学生中,活动开展前阅读量不超过1.5h的学生大约有1300名;活动开展后阅读量超过1.5h的学生大约有2350名.
 已知:如图,O是△ABC的内角∠ABC和外角∠ACE的平分线的交点.
已知:如图,O是△ABC的内角∠ABC和外角∠ACE的平分线的交点.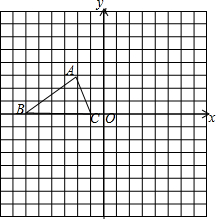 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).