题目内容
13.已知关于x的一元二次方程x2-3x+m=0有两个不相等的实数根x1、x2.(1)求m的取值范围;
(2)当x1=1时,求另一个根x2的值.
分析 (1)根据题意可得根的判别式△>0,再代入可得9-4m>0,再解即可;
(2)根据根与系数的关系可得x1+x2=-$\frac{b}{a}$,再代入可得答案.
解答 解:(1)由题意得:△=(-3)2-4×1×m=9-4m>0,
解得:m<$\frac{9}{4}$;
(2)∵x1+x2=-$\frac{b}{a}$=3,x1=1,
∴x2=2.
点评 此题主要考查了根与系数的关系,以及根的判别式,关键是掌握一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.

练习册系列答案
相关题目
3.下列说法错误的是( )
| A. | 三角形中至少有两个锐角 | |
| B. | 两条边及一角对应相等的三角形全等 | |
| C. | 两个角及一边对应相等的三角形全等 | |
| D. | 三角形的外角大于不相邻的内角 |
 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D=35°.
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D=35°. 如图,这是一个供滑板爱好者滑行使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=8m,点E在CD上,CE=2m,一位滑行爱好者从A点到E点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)
如图,这是一个供滑板爱好者滑行使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=8m,点E在CD上,CE=2m,一位滑行爱好者从A点到E点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)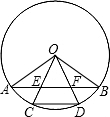 如图,OA、OB是⊙O的两条半径,且OA⊥OB,C、D是$\widehat{AB}$的三等两点,OC、OD分别交AB于E、F,则AE、CD与BF相等吗?为什么?
如图,OA、OB是⊙O的两条半径,且OA⊥OB,C、D是$\widehat{AB}$的三等两点,OC、OD分别交AB于E、F,则AE、CD与BF相等吗?为什么?