题目内容
我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．请解答下列问题：
（1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；
（2）探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论．
（1）梯形、矩形、正方形；（2）答案见解析
【解析】试题分析：（1）等腰梯形、矩形、正方形，任选两个即可；
（2）等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和大于或等于一条对角线的长．分两种情况证明：当BC与CE不在同一条直线上时，60°角所对的两边之和大于其中一条对角线的长；当BC与CE在同一条直线上时60°角所对的两边之和等于其中一条对角线的长．
...
某次数学测验，共有16道选择题，评分方法是：答对一题得6分，不答或答错一题扣2分．某同学要想得分为60分以上，他至少应答对多少道题?(只列关系式)
6x－2(16－x)≥60
【解析】试题分析：关系式为：6×答对的题数-2×其余题数≥60，据此列不等式即可.
试题解析：设该同学应答对x道题，依题意得
6x－2(16－x) ≥60. 已知∠AOB＝30°，点P在∠AOB的内部，点P1和点P关于OA对称，点P2和点P关于OB对称，则P1、O、P2三点构成的三角形是（ ）
A. 直角三角形 B. 钝角三角形 C. 等腰直角三角形 D. 等边三角形
D
【解析】
连接OP，
∵点P1和点P关于OA对称，点P2和点P关于OB对称，
∴OA垂直平分PP1，OB垂直平分PP2，
∴OP=OP1，OP=OP2，
∴OP1=OP2，∠P1OA=∠AOP，∠P2OB=∠BOP，
∵∠AOB=30°，
∴∠P1O P2=∠P1O P+∠P2O P=2∠AOP+2∠BOP=2（∠AOP+∠BOP）=2∠AOB=... 已知互不平行的两条线段AB，CD关于直线l对称，AB，CD所在直线交于点P，下列结论中：①AB=CD；②点P在直线l上； ③若A、C是对称点，则l垂直平分线段AC； ④若B、D是对称点，则PB=PD.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
D
【解析】由抽对称的性质知，①②③④都正确.
故选D. 观察下列平面图形：其中属于轴对称图形的有( )
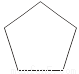
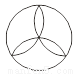
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】根据轴对称图形的定义可知，前三个图形分别有5条、5条、3条对称轴，最后一个图形三角形内的图案没有对称轴.
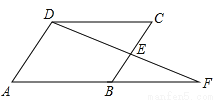
故选C. 如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于F点，CD∥AF，请你添加一个条件：_________使四边形ABCD是平行四边形
AB=BF
【解析】添加条件是AB=BF，求出∠CDE=∠F，CE=BE，根据AAS证△CDE≌△BFE，推出DC=BF，推出AB=CD，CD∥AB，根据平行四边形的判定推出即可． 根据下列条件，能作出平行四边形的是（ ）
A. 两组对边的长分别是3和5
B. 相邻两边的长分别是3和5，且一条对角线长为9
C. 一边的长为7，两条对角线的长分别为6和8
D. 一边的长为7，两条对角线的长分别为6和5
A
【解析】解：A．因为平行四边形的对边相等，故本选项正确；
B．因为3+5＜9，根据三角形的三边关系定理不能作出三角形，也不能作出平行四边形，故本选项错误；
C．因为3+4=7，根据三角形的三边关系定理不能作出三角形，也不能作出平行四边形，故本选项错误；
D．因为3+2.5＜7，根据三角形的三边关系定理不能作出三角形，也不能作出平行四边形，故本选项错误；
故选A．
... 下列每一个不透明袋子中都装有若干个红球和白球(除颜色外其他均相同).
第一个袋子:红球1个,白球1个;
第二个袋子:红球1个,白球2个;
第三个袋子:红球2个,白球3个;
第四个袋子:红球4个,白球10个.
分别从中任意摸出一个球,摸到红球的可能性最大的是( )
A. 第一个袋子 B. 第二个袋子
C. 第三个袋子 D. 第四个袋子
A
【解析】要求可能性的大小，只需求出各自所占的比例大小即可．求比例时，应注意记清各自的数目．
【解析】
第一个袋子摸到红球的可能性=；
第二个袋子摸到红球的可能性=；
第三个袋子摸到红球的可能性=；
第四个袋子摸到红球的可能性==．
故选A． 分式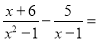
____________
【解析】试题分析：原式＝
＝
＝
＝．
故答案为： ．