题目内容
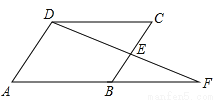
如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于F点，CD∥AF，请你添加一个条件：_________使四边形ABCD是平行四边形
AB=BF
【解析】添加条件是AB=BF，求出∠CDE=∠F，CE=BE，根据AAS证△CDE≌△BFE，推出DC=BF，推出AB=CD，CD∥AB，根据平行四边形的判定推出即可．
练习册系列答案
相关题目
用不等式表示下列关系：
（1）一个数的平方是非负数；（2）某天的气温不高于 25℃．
（1）x2≥0；（2）x≤25．
【解析】试题分析：（1）非负数则表示为“大于或等于0的数”；
（2）不高于则表示为“小于或等于”，用数学符号表示即可．
试题解析：（1）设这个数为x，则x2≥0；
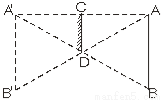
（2）设某天的气温为x℃， 则x≤25． 小红想在卧室放一穿衣镜，能看到自己的全身像，那么她至少应买多高(宽度适当)的穿衣镜？
镜高至少为身高的一半
【解析】试题分析：设小红用线段AB表示，则A头部，通过镜子下沿D处可以看到自己的脚的映像，而根据轴对称的性质，可以通过镜子顶端C处看到自己的头部映像，因此，镜子调试至少需要自己身体的一半高度.
【解析】
由轴对称的性质得CA=CA′，
∵CD∥AB,
∴CD为△AA′B的中位线 ，
∴镜子高度至少为身高的一半． 如果一个三角形是轴对称图形，且有一个内角是60°,那么这个三角形是( )
A. 等边三角形 B. 等腰直角三角形 C. 等腰三角形 D. 含30°角的直角三角形
A
【解析】∵这个三角形是轴对称图形 ，
∴一定有两个角相等，
∴这是一个等腰三角形.
∵有一个内角是60°，
∴这个三角形是等边三角形.
故选A. 我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．请解答下列问题：
（1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；
（2）探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论．
（1）梯形、矩形、正方形；（2）答案见解析
【解析】试题分析：（1）等腰梯形、矩形、正方形，任选两个即可；
（2）等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和大于或等于一条对角线的长．分两种情况证明：当BC与CE不在同一条直线上时，60°角所对的两边之和大于其中一条对角线的长；当BC与CE在同一条直线上时60°角所对的两边之和等于其中一条对角线的长．
... 如图,已知△ABC，别以A、C为圆心，BC，AB长为半径画弧，两弧在直线BC上方交于点D，连结AD，CD，则有( )
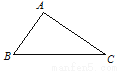
A. ∠ADC与∠BAD相等 B. ∠ADC与∠BAD互补
C. ∠ADC与∠ABC互补 D. ∠ADC与∠ABC互余
B
【解析】如图，依题意得AD=BC、CD=AB，∴四边形ABCD是平行四边形，∴∠ADC+∠BAD=180°，∠ADC=∠ABC，∴B正确． 下列选项中的四边形只有一个为平行四边形，根据图中所给的边长长度及角度，判断哪一个为平行四边形？（ ）
A. 
B. 
C.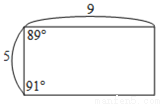 
D.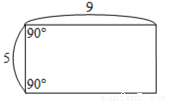 
B
【解析】解：A．上、下这一组对边平行，可能为等腰梯形；
B．上、下这一组对边平行，可能为等腰梯形，但此等腰梯形底角为90°，所以为平行
四边形；
C．上、下这一组对边平行，可能为梯形；
D．上、下这一组对边平行，可能为梯形；
故选B． 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
A. 至少有1个球是黑球
B. 至少有1个球是白球
C. 至少有2个球是黑球
D. 至少有2个球是白球
A
【解析】试题分析：根据必然事件、不可能事件、随机事件的概念进行判断即可．
至少有1个球是黑球是必然事件，A正确；
至少有1个球是白球是随机事件，B错误；
至少有2个球是黑球是随机事件，C错误；
至少有2个球是白球是随机事件，D错误，
故选：A． 已知x－y=xy,则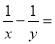
_______________.
－1
【解析】试题分析：
＝
＝
＝
＝－1．
故答案为－1．