题目内容
某次数学测验，共有16道选择题，评分方法是：答对一题得6分，不答或答错一题扣2分．某同学要想得分为60分以上，他至少应答对多少道题?(只列关系式)
6x－2(16－x)≥60
【解析】试题分析：关系式为：6×答对的题数-2×其余题数≥60，据此列不等式即可.
试题解析：设该同学应答对x道题，依题意得
6x－2(16－x) ≥60.
练习册系列答案
相关题目
若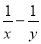
=3 ，求
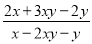的值．
【解析】分析：由已知可知x-y=-3xy，然后代入所求的式子，进行约分就可求出结果．
本题解析：
∵ =3，∴y-x=3xy, ∴x-y=-3xy,
∴ =. 设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（ ）
A. a＞b B. a=b C. a＜b D. b=a+180°
B
【解析】∵四边形的内角和等于a，
∴a=（4﹣2）•180°=360°．
∵五边形的外角和等于b，
∴b=360°，
∴a=b．
故选B． 如图，AC、BD是四边形ABCD的对角线，E、F分别是AD、BC的中点，M、N分别是BD、AC的中点．
求证：EF与MN互相平分．
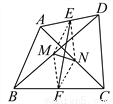
证明见解析.
【解析】试题分析：连接EM、EN、FM、FN，证明四边形EMFN为平行四边形，根据平行四边形对角线互相平分即可得.
试题解析：连接EM、EN、FM、FN，
∵E为AD的中点，N为AC的中点，
∴EN是△ACD的是位线，
∴EN∥CD，EN＝CD，
同理MF∥CD，MF＝CD，
∴EN∥MF，EN＝MF，
∴四边形EMFN为平行四边形，
... 如图，在△ABC中，∠ACB=90°，AC=8，AB="10." DE垂直平分AC交AB于点E，则DE的长为（ ）
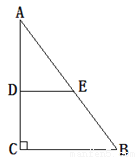
A. 6 B. 5 C. 4 D. 3
D
【解析】试题分析：已知，在△ABC中，∠ACB=90°，AC=8，AB=10，根据勾股定理可得BC=6，又因DE垂直平分AC，∠ACB=90°，可得DE为△ABC的中位线，根据三角形的中位线定理可得DE=BC=3，故答案选D. 用不等式表示下列关系：
（1）一个数的平方是非负数；（2）某天的气温不高于 25℃．
（1）x2≥0；（2）x≤25．
【解析】试题分析：（1）非负数则表示为“大于或等于0的数”；
（2）不高于则表示为“小于或等于”，用数学符号表示即可．
试题解析：（1）设这个数为x，则x2≥0；
（2）设某天的气温为x℃， 则x≤25． 用不等号连接下列各对数：（1）-
_______-
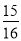，（2）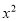 
+1 _______0 ．
> >
【解析】（1）∵， ，∴，
故答案为：>；
（2）∵x2≥0，∴x2+1>0，
故答案为：>. 下列说法正确的有( )个
①有一个外角是120°的等腰三角形是等边三角形．
②有两个外角相等的等腰三角形是等边三角形．
③有一边上的高也是这边上的中线的等腰三角形是等边三角形．
④三个外角都相等的三角形是等边三角形．
A. 4个 B. 3个 C. 2个 D. 1个
C
【解析】利用等腰三角形和等边三角形的性质及判定即可得出答案.
【解析】
①有一个外角是120°则其相邻的内角为60°，又是等腰三角形，所以必定是等边三角形，正确；
②有两个外角相等，则与这两个外角相邻的内角也相等，但是如果这两个内角就是原来等腰三角形的两个底角，则不能判定是等边三角形；故错误；
③有一边上的高也是这边上的中线，如果这条边恰好是原等腰三角形的底边，则不能... 我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．请解答下列问题：
（1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；
（2）探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论．
（1）梯形、矩形、正方形；（2）答案见解析
【解析】试题分析：（1）等腰梯形、矩形、正方形，任选两个即可；
（2）等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和大于或等于一条对角线的长．分两种情况证明：当BC与CE不在同一条直线上时，60°角所对的两边之和大于其中一条对角线的长；当BC与CE在同一条直线上时60°角所对的两边之和等于其中一条对角线的长．
...