题目内容
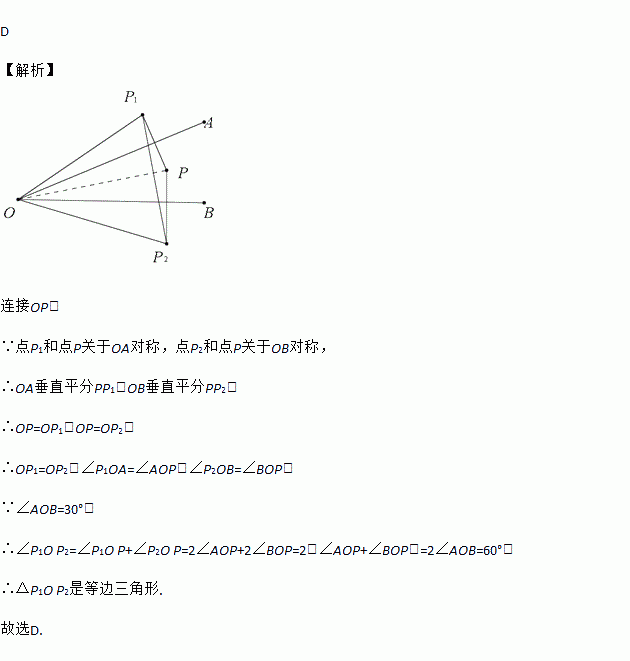
已知∠AOB＝30°，点P在∠AOB的内部，点P1和点P关于OA对称，点P2和点P关于OB对称，则P1、O、P2三点构成的三角形是（ ）
A. 直角三角形 B. 钝角三角形 C. 等腰直角三角形 D. 等边三角形
D
【解析】
连接OP，
∵点P1和点P关于OA对称，点P2和点P关于OB对称，
∴OA垂直平分PP1，OB垂直平分PP2，
∴OP=OP1，OP=OP2，
∴OP1=OP2，∠P1OA=∠AOP，∠P2OB=∠BOP，
∵∠AOB=30°，
∴∠P1O P2=∠P1O P+∠P2O P=2∠AOP+2∠BOP=2（∠AOP+∠BOP）=2∠AOB=...
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（ ）
A. a＞b B. a=b C. a＜b D. b=a+180°
B
【解析】∵四边形的内角和等于a，
∴a=（4﹣2）•180°=360°．
∵五边形的外角和等于b，
∴b=360°，
∴a=b．
故选B． 用不等号连接下列各对数：（1）-
_______-
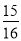，（2）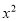 
+1 _______0 ．
> >
【解析】（1）∵， ，∴，
故答案为：>；
（2）∵x2≥0，∴x2+1>0，
故答案为：>. 下列说法正确的有( )个
①有一个外角是120°的等腰三角形是等边三角形．
②有两个外角相等的等腰三角形是等边三角形．
③有一边上的高也是这边上的中线的等腰三角形是等边三角形．
④三个外角都相等的三角形是等边三角形．
A. 4个 B. 3个 C. 2个 D. 1个
C
【解析】利用等腰三角形和等边三角形的性质及判定即可得出答案.
【解析】
①有一个外角是120°则其相邻的内角为60°，又是等腰三角形，所以必定是等边三角形，正确；
②有两个外角相等，则与这两个外角相邻的内角也相等，但是如果这两个内角就是原来等腰三角形的两个底角，则不能判定是等边三角形；故错误；
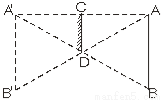
③有一边上的高也是这边上的中线，如果这条边恰好是原等腰三角形的底边，则不能... 桌面上有A、B两球，若要将B球射向桌面任意一边，使一次反弹后击中A，则如图所示8个点中，可以瞄准的点的个数（ ）
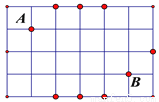
A. 1 B. 2 C. 4 D. 6
B
【解析】利用轴对称的性质准确画出图形即可得出答案.
【解析】
要想一次反弹后击中A，需要入射角也反射角相等，因此，可以经过如下图所示的两条路径达到要求，即B-D-A或者B-C-A，另外的一次反弹路线，都不经过图中给出的点，故选B. 小红想在卧室放一穿衣镜，能看到自己的全身像，那么她至少应买多高(宽度适当)的穿衣镜？
镜高至少为身高的一半
【解析】试题分析：设小红用线段AB表示，则A头部，通过镜子下沿D处可以看到自己的脚的映像，而根据轴对称的性质，可以通过镜子顶端C处看到自己的头部映像，因此，镜子调试至少需要自己身体的一半高度.
【解析】
由轴对称的性质得CA=CA′，
∵CD∥AB,
∴CD为△AA′B的中位线 ，
∴镜子高度至少为身高的一半． 设A、B两点关于直线MN轴对称,则_______垂直平分________.
直线MN 线段AB
【解析】∵A、B两点关于直线MN轴对称，
∴由轴对称的性质可得，直线MN垂直平分线段AB. 我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．请解答下列问题：
（1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；
（2）探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论．
（1）梯形、矩形、正方形；（2）答案见解析
【解析】试题分析：（1）等腰梯形、矩形、正方形，任选两个即可；
（2）等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和大于或等于一条对角线的长．分两种情况证明：当BC与CE不在同一条直线上时，60°角所对的两边之和大于其中一条对角线的长；当BC与CE在同一条直线上时60°角所对的两边之和等于其中一条对角线的长．
... 计算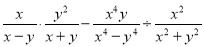
【解析】试题分析：分式乘除法和减法的混合运算应根据运算顺序先算乘除后算加减.
试题解析：
原式=