题目内容
2.在平面直角坐标系中,有A(2,-1),B(3,1)两点,现另取一点C(1,n),当n=-3时,|AC-BC|的值最大.分析 先求出直线AB的解析式,再求出直线AB与x=1的交点即可.
解答 解:连接AB并延长,交x=1于点C,
任取一点C',连接AC'、BC',
在△ABC'中,根据三角形的性质,两边之差小于第三边,
即AC'-BC'<AB,
∴可知AB为所求的最大值.
设直线AB的解析式为:y=kx+b,则
$\left\{\begin{array}{l}{2k+b=-1}\\{3k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-5}\end{array}\right.$,
∴y=2k-5,
把C(1,n)代入y=2k-5,得n=-3.
点评 本题主要考查了一次函数的应用、三角形的性质,正确理解|AC-BC|的值最大是解决问题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13.二元一次方程组$\left\{\begin{array}{l}{x+2y=1}\\{x-y=-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ |
10.有A、B两个黑色袋子,A袋装有3个黑球、2个白球,B袋装有黑、白两个球,这些球除颜色外,其它一样.在随机抽球中,如果从A袋取一个球,再从B袋取一个球,那么得到两个都是黑球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
7.矩形的边长为10和15,其中一个内角平分线分长边为两部分,这两部分的长度分别为( )
| A. | 6和9 | B. | 5和10 | C. | 4和11 | D. | 7和8 |
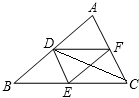 如图所示,在△ABC中,D,E,F分别为边AB,BC,CA的中点,连接DE,DF,CD,EF,请你判断CD和EF的位置关系,并证明.
如图所示,在△ABC中,D,E,F分别为边AB,BC,CA的中点,连接DE,DF,CD,EF,请你判断CD和EF的位置关系,并证明. 如图四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发以1cm/s的速度向D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.
如图四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发以1cm/s的速度向D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.