题目内容
10．有A、B两个黑色袋子，A袋装有3个黑球、2个白球，B袋装有黑、白两个球，这些球除颜色外，其它一样．在随机抽球中，如果从A袋取一个球，再从B袋取一个球，那么得到两个都是黑球的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{5}$ | D． | $\frac{3}{10}$ |
分析 分别求得各自袋子中摸到黑球的概率，然后相乘即可得到两个袋子均为黑球的概率．
解答 解：∵A袋装有3个黑球、2个白球，B袋装有黑、白两个球，
∴A袋中摸到黑球的概率为$\frac{3}{5}$，B袋中摸到黑球的概率为$\frac{1}{2}$，
∴P（两个都是黑球）=$\frac{3}{5}$×$\frac{1}{2}$=$\frac{3}{10}$，
故选D．
点评 本题考查了组合概率的求法，解题的关键是了解两个独立事件同时发生的概率等于两个独立事件发生概率的积，难度不大．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
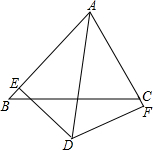已知在△ABC中，∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB于点E，DF⊥AC交AC的延长线于点F，求证：BE=CF．