题目内容
7．矩形的边长为10和15，其中一个内角平分线分长边为两部分，这两部分的长度分别为（ ）| A． | 6和9 | B． | 5和10 | C． | 4和11 | D． | 7和8 |
分析 作出草图，根据角平分线的定义求出∠BAE=45°，然后判断出△ABE是等腰直角三角形，然后求出BE=AB，再求出CE即可得解．
解答 解：如图，∵AE平分∠BAD，
∴∠BAE=45°，
又∵∠B=90°，
∴△ABE是等腰直角三角形，
∴BE=AB=10，
∴CE=BC-AB=15-10=5，
即这两部分的长为5和10．
故选B．
点评 本题考查了矩形的性质，角平分线的定义，熟记性质判断出△ABE是等腰直角三角形是解题的关键．
练习册系列答案
相关题目
如图，在△ABC的一边AB上有一点P．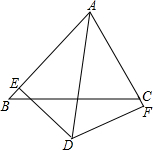
已知在△ABC中，∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB于点E，DF⊥AC交AC的延长线于点F，求证：BE=CF．