题目内容
11．
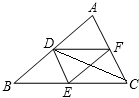如图所示，在△ABC中，D，E，F分别为边AB，BC，CA的中点，连接DE，DF，CD，EF，请你判断CD和EF的位置关系，并证明．
分析 先由中位线定理得到DF∥BC，DF=$\frac{1}{2}$BC=EC，再利用一组对边平行且相等的四边形是平行四边形进行平行四边形的判定．最后根据平行四边形的性质判断CD和EF的位置关系．
解答 解：CD和EF互相平分．
理由：∵D、F分别为边AB、CA的中点．
∴DF∥BC，DF=$\frac{1}{2}$BC，
∵E为边BC的中点
∴EC=$\frac{1}{2}$BC，
∴DF=EC，
∴四边形DECF是平行四边形，
∴CD和EF互相平分．
点评 主要考查了平行四边形的判定及性质和三角形中位线定理，掌握平行四边形的判定和性质定理以及三角形中位线定理是解题的关键．
练习册系列答案
相关题目
如图，在直角坐标系中，矩形OABC的两边在坐标轴上，其中点B的坐标为（4，3），过点A的直线AD的解析式为y=2x+3，点P是直线AD上一动点，点Q是线段BC（包括B，C两点）上一动点．
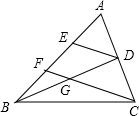如图，△ABC中，D为AC的中点，E，F为AB的三等分点，且DE∥FC，CF交BD于G，求证：BG=GD．