如果x是m.n的比例中项(即x2=m•n).求$\frac{1}{{m}^{2}-{x}^{2}}$+$\frac{1}{{n}^{2}-{x}^{2}}$+$\frac{1}{{x}^{2}}$的值．题目和参考答案——青夏教育精英家教网—

题目内容

14．如果x是m，n的比例中项（即x²=m•n），求$\frac{1}{{m}^{2}-{x}^{2}}$+$\frac{1}{{n}^{2}-{x}^{2}}$+$\frac{1}{{x}^{2}}$的值．

分析直接把x²=m•n代入进行计算即可．

解答解：∵x是m，n的比例中项，
∴原式=$\frac{1}{{m}^{2}-mn}$+$\frac{1}{{n}^{2}-mn}$+$\frac{1}{mn}$
=$\frac{1}{m（m-n）}$-$\frac{1}{n（m-n）}$+$\frac{1}{mn}$
=$\frac{n-m+m-n}{nm（m-n）}$
=0．

点评本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

练习册系列答案

相关题目

4．

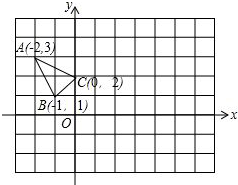如图所示，在平面直角坐标系中△ABC三个顶点的坐标分别是点A（-2，3）、点B（-1，1）、点C（0，2）．
（1）作△ABC关于C成中心对称的△A₁B₁C₁；
（2）将△A₁B₁C₁向右平移3个单位，作出平移后的△A₂B₂C₂；
（3）在x轴上求作一点P，使PA₁+PC₁的值最小，并写出点 P 的坐标．（不写解答过程，直接写出结果）

5．在一个不透明的袋子中，放有四张质地完全相同的卡片，分别标有数字1，2，3，4．第一次从袋中随机地抽出一张卡片，把其上的数字记为横坐标x，然后把卡片放回袋中，搅匀后第二次再随机地从中抽出一张，把其上的数字记为纵坐标y．
（1）用树状图或列表法把所有可能的点表示出来；
（2）求所得的点在直线y=-x+5的点的概率．

2．在平面直角坐标系中，有A（2，-1），B（3，1）两点，现另取一点C（1，n），当n=-3时，|AC-BC|的值最大．

9．此题出自中国元代朱世杰所著的《四元玉鉴》，题意是：用6210钱请人去买椽子，每株椽子的运费为3钱，总的运费正好等于一株椽子的价钱．椽价和椽数各多少？

19．试说明不论a取何值，方程（a²-2a+2）x²+ax+1=0都是一元二次方程．

6．已知y=$\sqrt{1-2x}$+$\sqrt{2x-1}$+$\sqrt{（x-1）^{2}}$，试求（4x-2y）²⁰¹⁵的值．

2．

如图，在直角坐标系中，矩形OABC的两边在坐标轴上，其中点B的坐标为（4，3），过点A的直线AD的解析式为y=2x+3，点P是直线AD上一动点，点Q是线段BC（包括B，C两点）上一动点．
（1）若AP=AQ且AP⊥AQ，求点P的坐标及AQ的解析式；
（2）以P，B，C为顶点作平行四边形PBEC，当对角线PE的值最小时，求点P的坐标；
（3）将直线y=2x+3向右平移3个单位，在该直线上存在点N，使△ANQ为等腰直角三角形，请直接写出平移后的直线解析式和满足条件的点N坐标．

3．下列各组数中，以a，b，c为边的三角形不是直角三角形的是（　　）

试题分类