题目内容
11. 如图四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发以1cm/s的速度向D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.
如图四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发以1cm/s的速度向D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.(1)直接写出,从运动开始经过6.5s,四边形ABQP是矩形;
(2)求从运动开始,使PQ=CD,需要经过多少时间?
分析 (1)由在梯形ABCD中,AD∥BC,∠B=90°,可得当AP=BQ时,四边形ABQP是矩形,即可得方程:t=26-2t,解此方程即可求得答案.
(2)根据PQ=CD,一种情况是:四边形PQCD为平行四边形,可得方程24-t=3t,一种情况是:四边形PQCD为等腰梯形,可求得当QC-PD=QC-EF=QF+EC=2CE,即3t-(24-t)=4时,四边形PQCD为等腰梯形,解此方程即可求得答案.
解答 解:根据题意得:AP=tcm,CQ=3tcm,
∵AB=8cm,AD=24cm,BC=26cm,
∴DP=AD-AP=24-t(cm),BQ=26-3t(cm),
(1)∵在梯形ABCD中,AD∥BC,∠B=90°,
∴当AP=BQ时,四边形ABQP是矩形,
∴t=26-3t,
解得:t=6.5,
∴当t=6.5时,四边形ABQP是矩形;
(2)若PQ=DC,分两种情况:
①PQ=DC,由(1)可知,t=6,
②PQ≠CC,由QC=PD+2(BC-AD),
可得方程:3t=24-t+4,
解得:t=7.
点评 此题考查了直角梯形的性质、平行四边形的判定、等腰梯形的判定以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
3.下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
| A. | a=3,b=4,c=5 | B. | a=6,b=8,c=10 | C. | a=2,b=3,c=3 | D. | a=1,b=1,c=$\sqrt{2}$ |
1.下列命题中的真命题是( )
| A. | 两个矩形一定相似 | |
| B. | 两个菱形一定相似 | |
| C. | 邻边之比为1:2的两个平行四边形相似 | |
| D. | 有一个角是60°的两个菱形相似 |
 如图,在直角坐标系中,矩形OABC的两边在坐标轴上,其中点B的坐标为(4,3),过点A的直线AD的解析式为y=2x+3,点P是直线AD上一动点,点Q是线段BC(包括B,C两点)上一动点.
如图,在直角坐标系中,矩形OABC的两边在坐标轴上,其中点B的坐标为(4,3),过点A的直线AD的解析式为y=2x+3,点P是直线AD上一动点,点Q是线段BC(包括B,C两点)上一动点.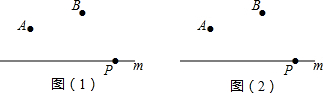
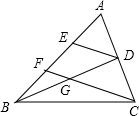 如图,△ABC中,D为AC的中点,E,F为AB的三等分点,且DE∥FC,CF交BD于G,求证:BG=GD.
如图,△ABC中,D为AC的中点,E,F为AB的三等分点,且DE∥FC,CF交BD于G,求证:BG=GD.