题目内容
9. 已知:如图,E是AC上一点,AB∥CD,∠B=∠CED,BC=ED.
已知:如图,E是AC上一点,AB∥CD,∠B=∠CED,BC=ED.(1)求证:AB=CE;
(2)若AB=5,AE=2,求CD长度.
分析 (1)根据两直线平行,内错角相等可得∠A=∠ECD,然后利用“角角边”证明△ABC和△ECD全等,再根据全等三角形对应边相等即可得证;
(2)根据AB=CE,AB=5,AE=2,求得AC=7,根据全等三角形的性质即可得到结论.
解答 (1)证明:∵AB∥CD,
∴∠A=∠ECD,
在△ABC和△ECD中,
$\left\{\begin{array}{l}{∠A=∠ECD}\\{∠B=∠CED}\\{BC=ED}\end{array}\right.$,
∴△ABC≌△ECD(AAS),
∴AB=CE;
(2)解:∵AB=CE,AB=5,AE=2,
∴AC=7,
∵△ABC≌△ECD,
∴CD=AC=7.
点评 本题考查了三角形全等的判定与性质,平行线的性质,比较简单,求出∠A=∠ECD是证明三角形全等的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,那么BC的长为( )
| A. | m•tanα•cosα | B. | m•cotα•cosα | C. | $\frac{m•tanα}{cosα}$ | D. | $\frac{m•tanα}{sinα}$ |
1.已知(m-n)2=32,(m+n)2=4000,则m2+n2的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 4032 |
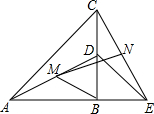 如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数.
如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数. 如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连按MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC;④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC;⑥将△BCE绕B点任意旋转到一个角度时,DN=AM总成立.正确的结论有①③④⑤(填写出所有正确的序号)
如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连按MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC;④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC;⑥将△BCE绕B点任意旋转到一个角度时,DN=AM总成立.正确的结论有①③④⑤(填写出所有正确的序号)