题目内容
3.已知等式3a=5b-1,则下列等式中不一定成立的是( )| A. | 3a-3=5b-4 | B. | 3a+b=6b-1 | C. | 3ac=5bc-1 | D. | b=$\frac{3a+1}{5}$ |
分析 根据等式的基本性质对各选项进行逐一分析即可.
解答 解:A、∵3a=5b-1,∴3a-3=5b-1-3,即3a-3=5b-4,故本选项正确;
B、∵3a=5b-1,∴3a+b=5b+b-1,即3a+b=6b-1,故本选项正确;
C、当c=0时,3ac=5bc-1不成立,故本选项错误;
D、∵3a=5b-1,∴3a+1=5b,∴b=$\frac{3a+1}{5}$,故本选项正确.
故选C.
点评 本题考查的是等式的性质,熟知等式的基本性质1是解答此题的关键.

练习册系列答案
相关题目
14.已知一元二次方程2x2+x+k=0无实数根,那么反比例函数y=$\frac{k}{x}$的图象位于( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一象限 | D. | 无法确定 |
8.若点(2,9)和(-3,a)都在某反比例函数的图象上,则a的值为( )
| A. | -6 | B. | 6 | C. | -2 | D. | 2 |
15.在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,那么BC的长为( )
| A. | m•tanα•cosα | B. | m•cotα•cosα | C. | $\frac{m•tanα}{cosα}$ | D. | $\frac{m•tanα}{sinα}$ |
 如图,在等边三角形ABC中AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,若BE=2,则AF=6.
如图,在等边三角形ABC中AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,若BE=2,则AF=6.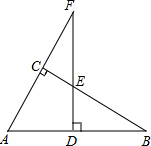 如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.
如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.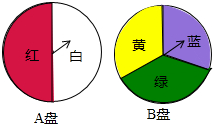 小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色.
小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色. 如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连按MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC;④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC;⑥将△BCE绕B点任意旋转到一个角度时,DN=AM总成立.正确的结论有①③④⑤(填写出所有正确的序号)
如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连按MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC;④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC;⑥将△BCE绕B点任意旋转到一个角度时,DN=AM总成立.正确的结论有①③④⑤(填写出所有正确的序号)