题目内容
4.△ABC是一张等腰直角三角形纸板,∠C=90°,AC=BC=2,在这张纸板中剪出一个尽可能大的正方形称为第1次剪取,记所得正方形面积s1(如图①);在余下的Rt△ADE和Rt△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2);继续操作下去…;则第2014次剪取时,S2014=$\frac{1}{{2}^{2013}}$.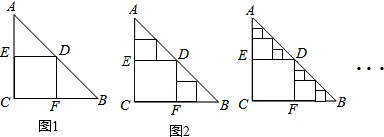
分析 根据题意,可求得S△AED+S△DBF=S正方形ECFD=S1=1,同理可得规律:Sn即是第n次剪取后剩余三角形面积和,根据此规律求解即可答案.
解答 解:∵四边形ECFD是正方形,
∴DE=EC=CF=DF,∠AED=∠DFB=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴AE=DE=EC=DF=BF=EC=CF,
∵AC=BC=2,
∴DE=DF=1,
∴S△AED+S△DBF=S正方形ECFD=S1=1;
同理:S2即是第二次剪取后剩余三角形面积和,
Sn即是第n次剪取后剩余三角形面积和,
∴第一次剪取后剩余三角形面积和为:2-S1=1=S1,
第二次剪取后剩余三角形面积和为:S1-S2=1-$\frac{1}{2}$=$\frac{1}{2}$=S2,
第三次剪取后剩余三角形面积和为:S2-S3=$\frac{1}{2}$-$\frac{1}{4}$=$\frac{1}{4}$=S3,
…
第n次剪取后剩余三角形面积和为:Sn-1-Sn=Sn=$\frac{1}{{2}^{n-1}}$.
则s2014=$\frac{1}{{2}^{2014-1}}=\frac{1}{{2}^{2013}}$,
故答案为:$\frac{1}{{2}^{2013}}$
点评 此题考查了正方形与等腰直角三角形的性质.此题难度较大,属于规律性题目,找到规律:Sn即是第n次剪取后剩余三角形面积和是解此题的关键.

练习册系列答案
相关题目
12.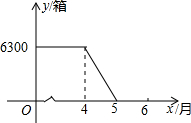 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
(1)从图象可知,该厂5月份开始出现零库存:此时日产销量为500箱;
(2)4月份总共的销售量为21300箱;
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于4月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
求:有几种购买设备的方案?若为了使日产量最大,应选择怎样的方案?
 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.(1)从图象可知,该厂5月份开始出现零库存:此时日产销量为500箱;
(2)4月份总共的销售量为21300箱;
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于4月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
| 型号 | A | B |
| 价格(万元/台) | 28 | 25 |
| 日产量(箱/台) | 50 | 40 |
9.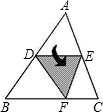 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )| A. | 55° | B. | 60° | C. | 70° | D. | 不能确定 |
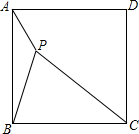 如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,
如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3, 如图,在两条交叉的公路L1与L2之间有两家工厂A、B,现在要修一个货物中转站,使它到两条公路的距离相等,以及到两个工厂距离相等,你能帮助确定中转站的地址吗?请试试.
如图,在两条交叉的公路L1与L2之间有两家工厂A、B,现在要修一个货物中转站,使它到两条公路的距离相等,以及到两个工厂距离相等,你能帮助确定中转站的地址吗?请试试.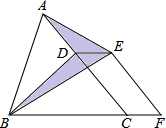 如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )