题目内容
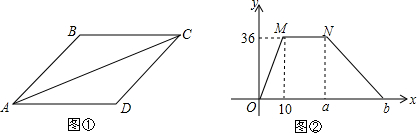
12.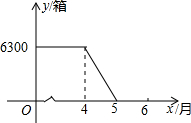 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.(1)从图象可知,该厂5月份开始出现零库存:此时日产销量为500箱;
(2)4月份总共的销售量为21300箱;
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于4月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
| 型号 | A | B |
| 价格(万元/台) | 28 | 25 |
| 日产量(箱/台) | 50 | 40 |
分析 (1)四月份以前,每天的产量与销售量均为500箱.而到5月份时,库存量为0,说明产量与销量相等;
(2)日销售量=库存量÷天数+500,总共的销售量等于日销售量×30,解答即可;
(3)关系式为:A型设备投资+B型设备投资≤135万元;新增机器的日产量≥710箱.
解答 解:(1)因为到5月份时,库存量为0,说明产量与销量相等,
可得:五月日产销量为:500,
故答案为:500;
(2)$\frac{6300}{30}=210$,
∴四月份的平均日销售量为210+500=710箱,
可得:总共的销售量=710×30=21300箱,
故答案为:21300;
(3)设购买A型设备x台,则购买B型设备(5-x)台,
根据题意,得:$\left\{\begin{array}{l}{28x+25(5-x)≤135}\\{50x+40(5-x)≥\frac{21300}{30}}\end{array}\right.$,
解得:$1≤x≤\frac{10}{3}$,
∴x=1、2、3,共有3种购买设备方案,
方案①:购买A型设备1台,购买B型设备4台
方案②:购买A型设备2台,购买B型设备3台
方案③:购买A型设备3台,购买B型设备2台
日产量Q=50x+40(5-x)+500=10x+700;
若选择①,日产量可增加50×1+40×4=210(箱)
若选择日产量可增加50×2+40×3=220(箱)
若选择③,日产量为50×3+40×2=230(箱)
∴选择方案③.
点评 本题考查了一次函数的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式组,确定具体方案是解决本题的关键,方案型问题是中考中经常出现的问题.

练习册系列答案
相关题目
7.现从A、B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
(2)设总运费为W元,请写出W与x的函数关系式;
(3)怎样调运蔬菜才能使运费最少?并求出最少的运费值.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
| 运往甲地(单位:吨) | 运往乙地(单位:吨) | |
| A | x | 14-x |
| B | 15-x | x-1 |
(3)怎样调运蔬菜才能使运费最少?并求出最少的运费值.
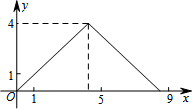
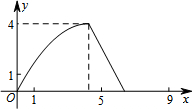
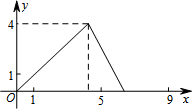
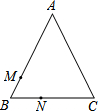 如图,在△ABC中,AB=AC,tan∠B=2,BC=3$\sqrt{2}$.边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°.设BE=x,MN=y,则能表示y与x的函数关系的大致图象是( )
如图,在△ABC中,AB=AC,tan∠B=2,BC=3$\sqrt{2}$.边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°.设BE=x,MN=y,则能表示y与x的函数关系的大致图象是( )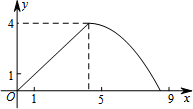
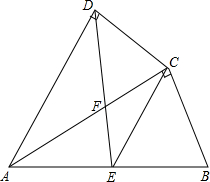 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.