题目内容
13.(1)计算:$\root{3}{27}$-(-1)2015×($\frac{1}{2}$)-2-|1-$\sqrt{2}$|(2)解方程:$\frac{1}{1-x}$=$\frac{3x-{x}^{2}}{1-{x}^{2}}$-1.
分析 (1)原式第一项利用立方根定义计算,第二项利用乘方的意义及负指数幂法则计算,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=3-(-1)×4-($\sqrt{2}$-1)=3+4-$\sqrt{2}$+1=8-$\sqrt{2}$;
(2)去分母得:1+x=3x-x2-1+x2,
解得:x=1,
经检验x=1是增根,分式方程无解.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8.某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转,某一指令规定:机器人先向前行走2米,然后左转45°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了( )
| A. | 14米 | B. | 15米 | C. | 16米 | D. | 17米 |
18.下列各式中正确的是( )
| A. | 若a>b,则a-1<b-1 | B. | 若a>b,则a2>b2 | ||
| C. | 若a>b,且c≠0,则ac>bc | D. | 若$\frac{a}{|c|}$>$\frac{b}{|c|}$,则a>b |
3.下列多项式的乘法,可以利用平方差公式计算的是( )
| A. | (a-b)(b-a) | B. | (-1-a)(a+1) | C. | (-m+n)(-m-n) | D. | (ax+b)(n-bx) |
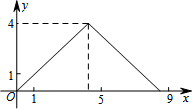
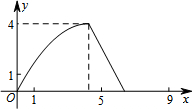
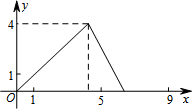
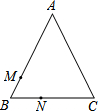 如图,在△ABC中,AB=AC,tan∠B=2,BC=3$\sqrt{2}$.边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°.设BE=x,MN=y,则能表示y与x的函数关系的大致图象是( )
如图,在△ABC中,AB=AC,tan∠B=2,BC=3$\sqrt{2}$.边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°.设BE=x,MN=y,则能表示y与x的函数关系的大致图象是( )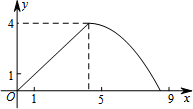
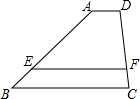 如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.
如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.