题目内容
15.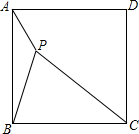 如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,
如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,(1)求∠APB的度数.
(2)求正方形ABCD的面积.
分析 (1)将△ABP绕点B按顺时针方向旋转90°,使AB与BC重合;则∠PBP′=90°,BP′=BP=2,P′C=PA=1;根据勾股定理得PP′2=22+22=8,再由P′C2=12=1,PC2=32=9可知PC2=PP′2+P′C2,根据∠APB=∠BP′C即可得出结论;
(2)过点B作BE⊥BP,且BE=BP,连接PE、CE、AC,则PE=$\sqrt{{BP}^{2}+{BE}^{2}}$=2$\sqrt{2}$.由SAS定理得出△ABP≌△CBE,故∠APB=∠CEB,CE=PA=1.根据∠APE=∠APB+∠BPE=180°可得出A、P、E三点共线,AE=PA+PE,再由S△ABC=S△PAB+S△PBC+S△PAC,S正方形ABCD=2S△ABC即可得出结论.
解答 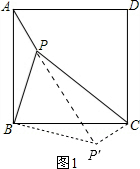 解:(1)如图1,将△ABP绕点B按顺时针方向旋转90°,使AB与BC重合;
解:(1)如图1,将△ABP绕点B按顺时针方向旋转90°,使AB与BC重合;
则∠PBP′=90°,BP′=BP=2,P′C=PA=1;
由勾股定理得:PP′2=22+22=8;
∵P′C2=12=1,PC2=32=9,
∴PC2=PP′2+P′C2,
∴∠PP′C=90°;而∠BP′P=45°,
∴∠BP′C=135°,∠APB=∠BP′C=135°;
(2)过点B作BE⊥BP,且BE=BP,连接PE、CE、AC,则PE=$\sqrt{{BP}^{2}+{BE}^{2}}$=2$\sqrt{2}$.
∵∠ABC=90°=∠PBE,
∴∠ABP=∠CBE.
∵AB=BC,BP=BE,
在△ABP与△CBE中,
∵$\left\{\begin{array}{l}AB=BC\\∠ABP=∠CBE\\ BP=BE\end{array}\right.$,
∴△ABP≌△CBE(SAS),
∴∠APB=∠CEB,CE=PA=1.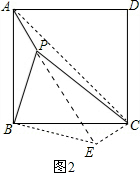
∵PE2+CE2=9=PC2,
∴∠PEC=90°,
∴∠APB=∠CEB=135°,
∴∠APE=∠APB+∠BPE=180°,
∴A、P、E三点共线,
∴AE=PA+PE=1+2$\sqrt{2}$,
∴S△ACE=$\frac{1}{2}$AE•CE=$\frac{1+2\sqrt{2}}{2}$,S△PBE=$\frac{1}{2}$PB•BE=2,
∴S△ABC=S△PAB+S△PBC+S△PAC
=S△EBC+S△PBC+S△PAC
=S△PBE+S△ACE
=$\frac{5+2\sqrt{2}}{2}$,
∴S正方形ABCD=2S△ABC=5+2$\sqrt{2}$.
点评 本题考查的是旋转的性质,熟知图形旋转不变性的性质是解答此题的关键.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案(1)设A地到甲地运送蔬菜x吨,请完成下表:
| 运往甲地(单位:吨) | 运往乙地(单位:吨) | |
| A | x | 14-x |
| B | 15-x | x-1 |
(3)怎样调运蔬菜才能使运费最少?并求出最少的运费值.
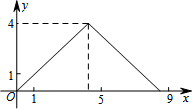
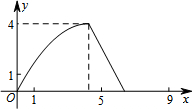
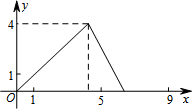
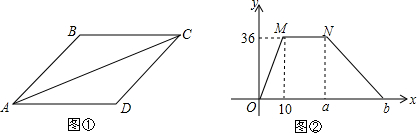
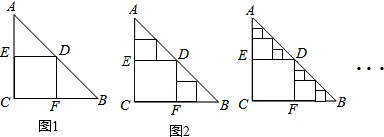
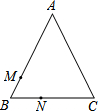 如图,在△ABC中,AB=AC,tan∠B=2,BC=3$\sqrt{2}$.边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°.设BE=x,MN=y,则能表示y与x的函数关系的大致图象是( )
如图,在△ABC中,AB=AC,tan∠B=2,BC=3$\sqrt{2}$.边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°.设BE=x,MN=y,则能表示y与x的函数关系的大致图象是( )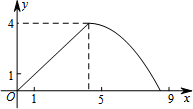
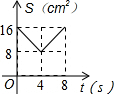
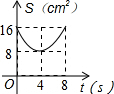
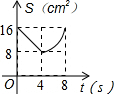
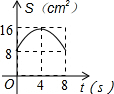
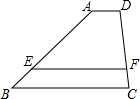 如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.
如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.