题目内容
16.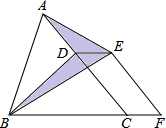 如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
分析 连接EC,过A作AM∥BC交FE的延长线于M,求出平行四边形ACFM,根据等底等高的三角形面积相等得出△BDE的面积和△CDE的面积相等,△ADE的面积和△AME的面积相等,推出阴影部分的面积等于平行四边形ACFM的面积的一半,求出CF×hCF的值即可.
解答 解:连接EC,过A作AM∥BC交FE的延长线于M,
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE边DE上的高和△CDE的边DE上的高相同,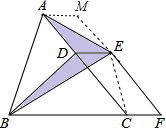
∴△BDE的面积和△CDE的面积相等,
同理△ADE的面积和△AME的面积相等,
即阴影部分的面积等于平行四边形ACFM的面积的一半,是$\frac{1}{2}$×CF×hCF,
∵△ABC的面积是24,BC=3CF
∴$\frac{1}{2}$BC×hBC=$\frac{1}{2}$×3CF×hCF=24,
∴CF×hCF=16,
∴阴影部分的面积是$\frac{1}{2}$×16=8,
故选:D.
点评 本题考查了平行四边形的性质和判定,三角形的面积的应用,主要考查学生的推理能力和转化能力,题目比较好,但是有一定的难度.

练习册系列答案
相关题目
7.现从A、B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
(2)设总运费为W元,请写出W与x的函数关系式;
(3)怎样调运蔬菜才能使运费最少?并求出最少的运费值.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
| 运往甲地(单位:吨) | 运往乙地(单位:吨) | |
| A | x | 14-x |
| B | 15-x | x-1 |
(3)怎样调运蔬菜才能使运费最少?并求出最少的运费值.
11.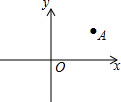 如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )
如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )
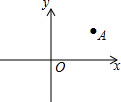 如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )
如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )| A. | (-2,3) | B. | (-3,2) | C. | (2,-3) | D. | (3,-2) |
8.某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转,某一指令规定:机器人先向前行走2米,然后左转45°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了( )
| A. | 14米 | B. | 15米 | C. | 16米 | D. | 17米 |
6.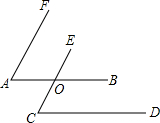 如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )
如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )
 如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )
如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )| A. | 30° | B. | 60° | C. | 80° | D. | 120° |
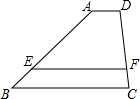 如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.
如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.