题目内容
1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对三角形的边分别为a,b,c.若a=3,b=4,则c=5,sinA=$\frac{3}{5}$,cosA=$\frac{4}{5}$,tanA=$\frac{3}{4}$,sinB=$\frac{4}{5}$,cosB=$\frac{3}{5}$,tanB=$\frac{4}{3}$.分析 结合锐角三角函数的定义和勾股定理进行解答即可.
解答 解:∵在Rt△ABC中,∠C=90°,a=3,b=4,
∴c=$\sqrt{{a}^{2}{+b}^{2}}$=5,
∴sinA=$\frac{a}{c}$=$\frac{3}{5}$,cosA=$\frac{b}{c}$=$\frac{4}{5}$,tanA=$\frac{a}{b}$=$\frac{3}{4}$,
sinB=$\frac{b}{c}$=$\frac{4}{5}$,cosB=$\frac{a}{c}$=$\frac{3}{5}$,tanB=$\frac{b}{a}$=$\frac{4}{3}$.
故答案为:5,$\frac{3}{5}$,$\frac{4}{5}$,$\frac{3}{4}$,$\frac{4}{5}$,$\frac{3}{5}$,$\frac{4}{3}$.
点评 本题考查了锐角三角函数的定义,解答本题的关键在于熟练掌握锐角三角函数的定义.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
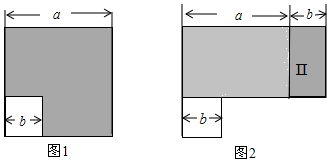
10.如图1,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图2.这个拼成的长方形的长为30,宽为20,则图2中Ⅱ部分的面积是( )

| A. | 60 | B. | 100 | C. | 125 | D. | 150 |
10.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见表:
已知4月份,该市居民甲用电250度,交电费130元;居民乙用电400度,交电费220元.
(1)求出表中a和b的值;
(2)实行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度不超过0.56元?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过200度 | a |
| 超过200度的部分 | b |
(1)求出表中a和b的值;
(2)实行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度不超过0.56元?
 如图,两条直线a、b相交,已知2∠3=3∠1,则∠2=108°.
如图,两条直线a、b相交,已知2∠3=3∠1,则∠2=108°. 如图,边长为8的等边△ABC,AD⊥BC于D,点E是线段AD上的一个动点,CF=CE,∠ECF=60°,则线段DF长的取值范围是4≤DF≤4$\sqrt{7}$.
如图,边长为8的等边△ABC,AD⊥BC于D,点E是线段AD上的一个动点,CF=CE,∠ECF=60°,则线段DF长的取值范围是4≤DF≤4$\sqrt{7}$. 现有八个大小相同的长方形,可拼成如图①、②所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,则每个小正方形的面积是60.
现有八个大小相同的长方形,可拼成如图①、②所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,则每个小正方形的面积是60.