题目内容
6．代数式a2+4b2-8a+4b+20的最小值3．分析 观察a2+4b2-8a+4b+20式子要求其最小值，只要将所有含有a、b的式子转化为多个非负数与常数项的和的形式．一般常数项即为所求最小值．
解答 解：a2+4b2-8a+4b+20
=（a2-8a+16）+（4b2+4b+1）+3
=（a-4）2+（2b+1）2+3≥3，
则代数式a2+4b2-8a+4b+20的最小值是3．
故答案是：3．
点评 本题考查了完全平方公式、非负数的性质．解决本题的关键是将所有含有a、b的式子都转化为多个非负数与常数项的和形式．
练习册系列答案
阅读快车系列答案
相关题目
17．
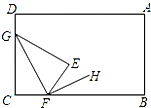如图所示，将一张长方形纸片AB-CD的∠C沿CF折叠（F在BC边上，不与B，C重合），使得C点落在长方形ABCD内部E处，FH平分∠BFE，则∠GFH的度数满足（ ）
如图所示，将一张长方形纸片AB-CD的∠C沿CF折叠（F在BC边上，不与B，C重合），使得C点落在长方形ABCD内部E处，FH平分∠BFE，则∠GFH的度数满足（ ）| A． | ∠GFH＜90° | B． | ∠GFH=90° | C． | ∠GFH＞90° | D． | 0°＜∠GFH＜90° |
如图所示，正方形ABCD的面积等于9平方厘米，正方形DEFG的面积等于4平方厘米，则阴影部分的面积S═3.5平方厘米．