题目内容
9. 如图,边长为8的等边△ABC,AD⊥BC于D,点E是线段AD上的一个动点,CF=CE,∠ECF=60°,则线段DF长的取值范围是4≤DF≤4$\sqrt{7}$.
如图,边长为8的等边△ABC,AD⊥BC于D,点E是线段AD上的一个动点,CF=CE,∠ECF=60°,则线段DF长的取值范围是4≤DF≤4$\sqrt{7}$.
分析 如图1,当点E运动到点D时,根据等边三角形的性质得到DF=CD=$\frac{1}{2}$BC=4;如图2,当点E运动到点A时,由已知条件得到△CEF是等边三角形,求得∠CEF=60°,AF=AC=8,根据等边三角形的性质得到∠DAC=30°,AD=4$\sqrt{3}$,根据勾股定理即可得到结论.
解答  解:如图1,当点E运动到点D时,
解:如图1,当点E运动到点D时,
∵CF=CE,∠ECF=60°,
∴点F在线段AC上,
∴△CDF是等边三角形,
∴DF=CD=$\frac{1}{2}$BC=4;
如图2,当点E运动到点A时,
∵CF=CE,∠ECF=60°,
∴△CEF是等边三角形,
∴∠CEF=60°,AF=AC=8,
∵△ABC是等边三角形,AD⊥BC,
∵∠DAC=30°,AD=4$\sqrt{3}$,
∴∠DAF=90°,
∴DF=$\sqrt{A{D}^{2}+A{F}^{2}}$=4$\sqrt{7}$,
∴线段DF长的取值范围是4≤DF≤4$\sqrt{7}$,
故答案为:4≤DF≤4$\sqrt{7}$.
点评 本题考查了等边三角形的性质,勾股定理,熟记等边三角形的性质是解题的关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
17.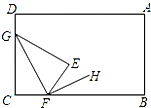 如图所示,将一张长方形纸片AB-CD的∠C沿CF折叠(F在BC边上,不与B,C重合),使得C点落在长方形ABCD内部E处,FH平分∠BFE,则∠GFH的度数满足( )
如图所示,将一张长方形纸片AB-CD的∠C沿CF折叠(F在BC边上,不与B,C重合),使得C点落在长方形ABCD内部E处,FH平分∠BFE,则∠GFH的度数满足( )
 如图所示,将一张长方形纸片AB-CD的∠C沿CF折叠(F在BC边上,不与B,C重合),使得C点落在长方形ABCD内部E处,FH平分∠BFE,则∠GFH的度数满足( )
如图所示,将一张长方形纸片AB-CD的∠C沿CF折叠(F在BC边上,不与B,C重合),使得C点落在长方形ABCD内部E处,FH平分∠BFE,则∠GFH的度数满足( )| A. | ∠GFH<90° | B. | ∠GFH=90° | C. | ∠GFH>90° | D. | 0°<∠GFH<90° |
 某小区有一块长方形的草地(如图),长18米,宽10米,空白部分为两条宽度均为2米的小路,则草地的实际面积128m2.
某小区有一块长方形的草地(如图),长18米,宽10米,空白部分为两条宽度均为2米的小路,则草地的实际面积128m2. 如图所示,正方形ABCD的面积等于9平方厘米,正方形DEFG的面积等于4平方厘米,则阴影部分的面积S═3.5平方厘米.
如图所示,正方形ABCD的面积等于9平方厘米,正方形DEFG的面积等于4平方厘米,则阴影部分的面积S═3.5平方厘米.