题目内容
14.已知y是x的反比例函数,下表给了一些x与y的一些值:| x | -3 | -2 | 4 |
| y | 4 | 6 | -3 |
(2)若点P(a,y)在该函数图象上,当y<2时,求a的取值范围.
分析 (1)设反比例函数解析式为y=$\frac{k}{x}$,然后把第二组数据代入进行计算即可求出k值,从而得解,再把x=-3与y=-3分别代入函数解析式进行计算即可得解;
(2)画出函数图象,然后根据反比例函数图象的增减性解答即可.
解答 解:(1)设该反比例函数解析式为y=$\frac{k}{x}$,
将x=-2,y=6代入解析式得,$\frac{k}{-2}$=6,
解得k=-12,
所以,该反比例函数的解析式为y=-$\frac{12}{x}$,
当x=-3时,y=-$\frac{12}{-3}$=4,
当y=-3时,-$\frac{12}{x}$=-3,解得x=4,
所以,表中空格:4,4;
(2)函数图象如图所示,
观察图象可得,当y<2时,a<-6或a>0.
点评 本题考查了待定系数法求反比例函数解析式,反比例函数图象的增减性,易错点在于反比例函数图象的增减性要分在每一个象限内.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5.关于反比例函数y=$\frac{2}{x}$的图象,下列说法正确的是( )
| A. | 图象经过点(1,1) | |
| B. | 当x<0时,y随x的增大而减小 | |
| C. | 图象的两个分支关于x轴成轴对称 | |
| D. | 图象的两个分支分布在第二、四象限 |
9.直线y1=2x+2关于x轴对称的直线为y2,则当y1>y2时,自变量x的取值范围是( )
| A. | x>-1 | B. | x<-1 | C. | x>2 | D. | x>0 |
6.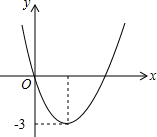 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
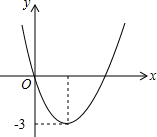 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )| A. | -3 | B. | 3 | C. | -6 | D. | 9 |
 如图,A点为反比例函数$y=\frac{k}{x}$图象上一点,过A点作AB⊥y轴,B为垂足,点P为x轴上任意一点,且△ABP的面积为2,则k=-4.
如图,A点为反比例函数$y=\frac{k}{x}$图象上一点,过A点作AB⊥y轴,B为垂足,点P为x轴上任意一点,且△ABP的面积为2,则k=-4. 如图,写出能判定AB∥CD的一对角的数量关系:∠BAC=∠ACD或∠B+∠BCD=180°或∠D+∠BAD=180°..
如图,写出能判定AB∥CD的一对角的数量关系:∠BAC=∠ACD或∠B+∠BCD=180°或∠D+∠BAD=180°..