题目内容
9.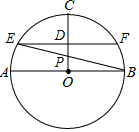 如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,EB与OC交于点P.
如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,EB与OC交于点P.(1)求∠ABE的度数.
(2)若连结AB=8,求EF的长.
分析 (1)连接OE,可得到△DOE为Rt△,由D为OC的中点,则可求出∠OED,于是得到∠AOE,利用圆周角定理即可求出∠ABE;
(2)由垂径定理和勾股定理求出DE,即可得出EF的长.
解答  解:连接OE,如图,
解:连接OE,如图,
∵半径CO垂直于直径AB,而EF∥AB,
∴∠EDO=90°,∠AOE=∠OED,
又∵D为OC的中点,
∴OD=$\frac{1}{2}$OC=$\frac{1}{2}$OE,
∴∠OED=30°,
∴∠AOE=30°,
∴∠ABE=$\frac{1}{2}$∠AOE=15°;
(2)∵EF∥AB,OC⊥AB,
∴OC⊥EF,
∴EF=2DE,
∵AB=8,
∴OE=OC=$\frac{1}{2}$AB=4,
∴OD=$\frac{1}{2}$OC=2,
∴DE=$\sqrt{{OE}^{2}-O{D}^{2}}$=2$\sqrt{3}$,
∴EF=4$\sqrt{3}$.
点评 本题考查了圆周角定理、垂径定理、勾股定理;熟练掌握圆周角定理是解决问题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
20. 如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
(1)填表:
(2)如果剪了100次,共剪出多少个小正方形?
(3)如果剪n次,共剪出多少个小正方形?
(4)如果要剪出100个正方形,那么需要剪多少次?
 如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.(1)填表:
| 剪的次数 | 1 | 2 | 3 | 4 | 5 |
| 正方形个数 | 4 | 7 | 10 | 13 | 16 |
(3)如果剪n次,共剪出多少个小正方形?
(4)如果要剪出100个正方形,那么需要剪多少次?
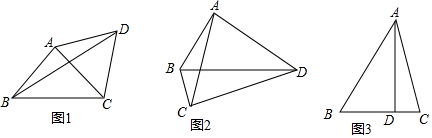
17. 如图,∠A+∠B+∠C+∠D+∠E的度数为( )
如图,∠A+∠B+∠C+∠D+∠E的度数为( )
 如图,∠A+∠B+∠C+∠D+∠E的度数为( )
如图,∠A+∠B+∠C+∠D+∠E的度数为( )| A. | 180o | B. | 270o | C. | 360o | D. | 540o |
18. 如图,有一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边有两个点,第三层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边有两个点,第三层每边有三个点,依此类推.
(1)填写表:
(2)写出第n层所对应的点数.
(3)如果某一层有96个点,请计算它是第几层?
 如图,有一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边有两个点,第三层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边有两个点,第三层每边有三个点,依此类推.(1)填写表:
| 层数 | 1 | 2 | 3 | 4 | … |
| 该层对应的点数 | 1 | 6 | 12 | 18 | … |
| 所有层的总点数 | 1 | 7 | 19 | 37 | … |
(3)如果某一层有96个点,请计算它是第几层?
 如图,是一个10×10的正方形网格,其中正方形的顶点称为格点,网格中△ABC的顶点A,B,C均在格点上,利用网格建立的平面直角坐标系中点A的坐标为(3,4).
如图,是一个10×10的正方形网格,其中正方形的顶点称为格点,网格中△ABC的顶点A,B,C均在格点上,利用网格建立的平面直角坐标系中点A的坐标为(3,4).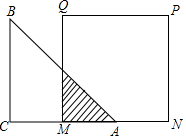 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合.
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合.