题目内容
19.已知正六边形的边心距为$\sqrt{3}$,则该正六边形的面积是6$\sqrt{3}$.分析 先求出正六边形的边心距,连接正六边形的一个顶点和中心可得到一直角三角形,解直角三角形求得边长,再求面积.
解答 解:作出正6边形的边心距, 连接正6边形的一个顶点和中心可得到一直角三角形,
连接正6边形的一个顶点和中心可得到一直角三角形,
在中心的直角三角形的角为360°÷6÷2=30°;
∴这个正6边形的边长的一半=$\sqrt{3}$×tan30°=1,
则边长为2,
面积为:6×$\frac{1}{2}$×2×$\sqrt{3}$=6$\sqrt{3}$.
故答案是:6$\sqrt{3}$.
点评 本题考查学生对正多边形的概念掌握和计算的能力.解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
10.若正实数a、b满足ab=a+b+3,则a2+b2的最小值为( )
| A. | -7 | B. | 2 | C. | 9 | D. | 18 |
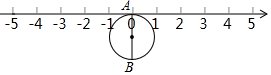 如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )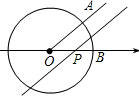 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是0<x≤$\sqrt{2}$.
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是0<x≤$\sqrt{2}$. 如图,已知△ABC,用直尺和圆规作△ABC的角平分线BD、高CE.(不必写画法,保留作图痕迹)
如图,已知△ABC,用直尺和圆规作△ABC的角平分线BD、高CE.(不必写画法,保留作图痕迹)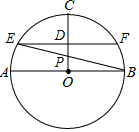 如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,EB与OC交于点P.
如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,EB与OC交于点P.