题目内容
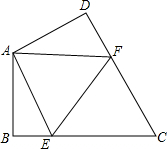 如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,BE=2,EF=5,则DF=
如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,BE=2,EF=5,则DF=考点:全等三角形的判定与性质,旋转的性质
专题:
分析:延长FD到M,使DM=BE,连接AM,根据SAS推出△ABE≌△ADM,根据全等得出AE=AM,∠BAE=∠D,求出∠MAF=∠EAF,根据SAS推出△EAF≌△MAF,根据全等得出EF=FM即可.
解答:解:
延长FD到M,使DM=BE,连接AM,
∵∠B=∠ADC=90°,
∴∠ADM=∠B=90°,
在△ABE和△ADM中
∴△ABE≌△ADM(SAS),
∴AE=AM,∠BAE=∠DAM,
∵∠BAD=120°,∠EAF=60°,
∴∠BAE+∠DAF=60°,
∴∠MAF=60°=∠EAF,
在△EAF和△MAF中
∴△EAF≌△MAF(SAS),
∴EF=FM,
∴DF=EF-BE=5-2=3,
故答案为:3.

延长FD到M,使DM=BE,连接AM,
∵∠B=∠ADC=90°,
∴∠ADM=∠B=90°,
在△ABE和△ADM中
|
∴△ABE≌△ADM(SAS),
∴AE=AM,∠BAE=∠DAM,
∵∠BAD=120°,∠EAF=60°,
∴∠BAE+∠DAF=60°,
∴∠MAF=60°=∠EAF,
在△EAF和△MAF中
|
∴△EAF≌△MAF(SAS),
∴EF=FM,
∴DF=EF-BE=5-2=3,
故答案为:3.
点评:本题考查了全等三角形的性质和判定的应用,能综合运用全等三角形的性质和判定进行推理是解此题的关键,注意:全等三角形的对应边相等.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
已知α,β是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足
+
=-1,则m的值是( )
| 1 |
| α |
| 1 |
| β |
| A、3 | B、1 |
| C、3或-1 | D、-3或1 |
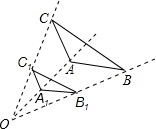 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为( )
如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为( )