题目内容

一个口袋中装有10个红球和若干个黄球，在不允许将球倒出来数的前提下，为估计口袋中黄球的个数，小明采用了如下的方法：每次先从口袋中摸出10个球，求出其中红球与10的比值，再把球放回口袋中摇匀．不断重复上述过程20次，得到红球数与10的比值的平均数为0.4．根据上述数据，估计口袋大约有（　　）个黄球．
A、7B、10C、15D、20
考点：利用频率估计概率
专题：
分析：在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，先求得红球的频率，再乘以总球数求解．
解答：解：∵小明通过多次摸球实验后发现其中摸到红色球的频率稳定在0.4，
设黄球有x个，
∴0.4（x+10）=10，
解得x=15．
故选C．
点评：考查了用频率估计概率，解答此题的关键是要估计出口袋中红色球所占的比例，得到相应的等量关系．
练习册系列答案
相关题目
阅读填空：
有一段长为180米的河道整治任务由A、B两个工程队先后接力完成．A工程队每天整治12米，B工程队每天整治8米．共用时20天．
根据题意，甲、乙两个同学分别列出尚不完整的方程组如下：
甲：
x+y=
12x+8y=

乙：
x+y=
x
12
+
y
8
=

（1）补全甲、乙两名同学所列的方程组；
（2）根据甲、乙两名同学所列的方程组，请你分别指出未知数x，y表示的意义：
甲：x表示
 
，y表示
 
；
乙：x表示
 
，y表示
 
．
如图，将三角尺的直角顶点放在直尺的一边上，∠1=20°，则∠2的度数等于（　　）
A、50°B、30°
C、20°D、15°
-
1
2
的倒数是（　　）
A、-2
B、2
C、
1
2
D、
1
4
抗战救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食全部转移到具有较强抗震功能的A、B两仓库，已知甲库有粮食80吨，乙库有粮食100吨，而A库的容量为110吨，B库的容量为70吨．从甲、乙两库到A、B两库的路程和运费如下表：（表中“元/吨•千米”表示每吨粮食运送1千米所需人民币）
路程（千米）运费（元/吨•千米）
甲库乙库甲库乙库
A库20151312
B库2520108
（1）若甲库运往A库粮食x吨，请写出将粮食运往A、B两库的总运费y（元）与x（吨）的函数关系式；
（2）当甲、乙两库各运往A、B两库多少吨粮食时，总运费最省，最省的总运费是多少？
计算：
（1）12-（-18）+（-7）-15；
（2）（-
1
2
）×（-8）+（-6）÷（-
1
3
）2．
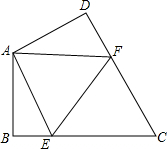如图，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，BE=2，EF=5，则DF=
 
．
在直角坐标系中描出下列各组点，并将各组内的点用线段依次连接起来．
①（-1，2），（0，0），（1，2）；
②（0，0），（4，3），（4，-1），（0，0）；
③（0，0），（-4，3），（-4，-1），（0，0）；
④（0，0），（2，-1.5），（2，-4），（0，0）；
⑤（0，0），（-2，-1.5），（-2，-4），（0，0）．
观察所得的图形，你觉得像什么？
函数y=-
1
3x
的图象与坐标轴的交点个数是（　　）
A、0个B、1个C、2个D、3个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网