题目内容

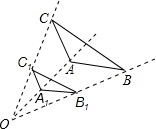如图，△ABC和△A1B1C1是以点O为位似中心的位似三角形，若C1为OC的中点，AB=4，则A1B1的长为（　　）
A、1B、2C、4D、8
考点：位似变换
专题：计算题
分析：根据位似变换的性质得到
A1B1
AB
=
OB1
OB
，B1C1∥BC，再利用平行线分线段成比例定理得到
OB1
OB
=
OC1
OC
，所以
A1B1
AB
=
OC1
OC
，然后把OC1=
1
2
OC，AB=4代入计算即可．
解答：解：∵C1为OC的中点，
∴OC1=
1
2
OC，
∵△ABC和△A1B1C1是以点O为位似中心的位似三角形，
∴
A1B1
AB
=
OB1
OB
，B1C1∥BC，
∴
OB1
OB
=
OC1
OC
，
∴
A1B1
AB
=
OC1
OC
，
即
A1B1
4
=
1
2

∴A1B1=2．
故选B．
点评：本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．注意：①两个图形必须是相似形；②对应点的连线都经过同一点；③对应边平行．
练习册系列答案
相关题目
数学课上，老师出示了如下框中的题目

小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况•探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系．请你直接写出结论：AE
 
DB（填“＞”，“＜”或“=”）．

（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是：AE
 
DB（填“＞”，“＜”或“=”）理由如下：如图2，过点E作EF∥BC，交AC于点F，（请你接着继续完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线上AB上，点D在直线BC上，且ED=EC．若△ABC的边长为3，AE=5，求CD的长（请你直接写出结果）．
抗战救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食全部转移到具有较强抗震功能的A、B两仓库，已知甲库有粮食80吨，乙库有粮食100吨，而A库的容量为110吨，B库的容量为70吨．从甲、乙两库到A、B两库的路程和运费如下表：（表中“元/吨•千米”表示每吨粮食运送1千米所需人民币）
路程（千米）运费（元/吨•千米）
甲库乙库甲库乙库
A库20151312
B库2520108
（1）若甲库运往A库粮食x吨，请写出将粮食运往A、B两库的总运费y（元）与x（吨）的函数关系式；
（2）当甲、乙两库各运往A、B两库多少吨粮食时，总运费最省，最省的总运费是多少？
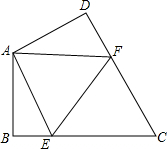如图，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，BE=2，EF=5，则DF=
 
．
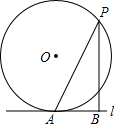如图，直线l与半径为2的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l，垂足为B，连接PA．设PA=x，PB=y，则（x-y）的最大值是
 
．
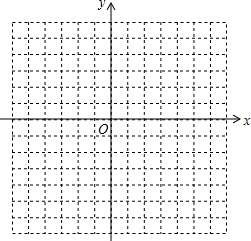在直角坐标系中描出下列各组点，并将各组内的点用线段依次连接起来．
①（-1，2），（0，0），（1，2）；
②（0，0），（4，3），（4，-1），（0，0）；
③（0，0），（-4，3），（-4，-1），（0，0）；
④（0，0），（2，-1.5），（2，-4），（0，0）；
⑤（0，0），（-2，-1.5），（-2，-4），（0，0）．
观察所得的图形，你觉得像什么？
如图，点D是△ABC的边AC上的一点，AB2=AC•AD．
求证：△ADB∽△ABC．
已知等边三角形的边长为2，一个顶点在原点，另一个顶点在y轴上，则它的第三个顶点的坐标为（　　）
A、（1，
3
），（-1，
3
）
B、（
3
，1），（
3
，-1）
C、（
3
，1），（
3
，-1)，（-
3
，1)（-
3
，-1)
D、（1，
3
），（-1，
3
），（1，-
3
），（-1，-
3
）
下面有5个说法：①单项式-πr2的系数是π；②多项式4α2-3-1的常数项是1；③1-
1
a
-
1
b
是多项式；④x6-1的项数和次数均为6；⑤
x2+1
3
不是单项式，其中正确的个数是（　　）
A、4个B、3个C、2个D、1个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网