题目内容
已知α,β是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足
+
=-1,则m的值是( )
| 1 |
| α |
| 1 |
| β |
| A、3 | B、1 |
| C、3或-1 | D、-3或1 |
考点:根与系数的关系
专题:计算题
分析:先根据根的判别式的意义可解得得m>-
,再根据根与系数的关系得到α+β=-(2m+3),αβ=m2,把
+
=-1变形得到
=-1,则
=-1,解得m1=3,m2=-1,然后根据m的取值范围确定m的值.
| 3 |
| 4 |
| 1 |
| α |
| 1 |
| β |
| α+β |
| αβ |
| -(2m+3) |
| m2 |
解答:解:根据题意得△=(2m+3)2-4m2>0,解得m>-
,
∵α+β=-(2m+3),αβ=m2,
而
+
=-1,
∴
=-1,
∴
=-1,
整理得m2-2m-3=0,解得m1=3,m2=-1,
而m>-
,
∴m的值为3.
故选A.
| 3 |
| 4 |
∵α+β=-(2m+3),αβ=m2,
而
| 1 |
| α |
| 1 |
| β |
∴
| α+β |
| αβ |
∴
| -(2m+3) |
| m2 |
整理得m2-2m-3=0,解得m1=3,m2=-1,
而m>-
| 3 |
| 4 |
∴m的值为3.
故选A.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
,x1•x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
已知等边三角形的边长为2,一个顶点在原点,另一个顶点在y轴上,则它的第三个顶点的坐标为( )
A、(1,
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(1,
|
函数y=-
的图象与坐标轴的交点个数是( )
| 1 |
| 3x |
| A、0个 | B、1个 | C、2个 | D、3个 |
要组织一次篮球邀请赛,参赛的每两个队都要比赛一场,根据场地和时间等条件,计划共安排28场比赛.设比赛组织共邀请x对参加比赛,则依题意可列方程为( )
A、
| ||
B、
| ||
| C、x(x-1)=28 | ||
| D、x(x+1)=28 |
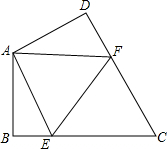 如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,BE=2,EF=5,则DF=
如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,BE=2,EF=5,则DF=