题目内容
如果点A,B在数轴上分别表示实数a,b; A,B两点之间的距离表示为|AB|,那么|AB|=|a-b|,根据这个公式解答下列问题:
(1)若数轴上A,B两点分别表示实数x和-
,且|AB|=5,则x= .
(2)若数轴上三点P,A,B分别表示实数x,-
和5,求当代数式|x+
|+|x-5|取最小值时,x的取值范围为 .
(1)若数轴上A,B两点分别表示实数x和-
| 3 |
(2)若数轴上三点P,A,B分别表示实数x,-
| 3 |
| 3 |
考点:实数与数轴,绝对值
专题:
分析:(1)根据数轴上两点间的距离公式可知AB=|x+
|=5,再根据绝对值的性质求出x的值即可;
(2)由线段的性质,两点之间,线段最短,可知当-
≤x≤5时,|x+
|+|x-5|有最小值
| 3 |
(2)由线段的性质,两点之间,线段最短,可知当-
| 3 |
| 3 |
解答:解:(1)∵数轴上A,B两点分别表示实数x和-
,且|AB|=5,
∴|x+
|=5,
当x+
≥0,即x≥-
时,原方程可化为x+
=5,解得x=5-
;
当x+
<0,即x<-
时,原方程可化为x+
=-5,解得x=-5-
,
综上所述,x=5-
或-5-
.
故答案为:5-
或-5-
.
(2)如图,代数式|x+
|+|x-5|取最小值时,即P到A、B的距离之和最小,
此时,P在A、B之间,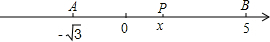
则-
≤x≤5.
故答案为5-
或-5-
,-
≤x≤5.
| 3 |
∴|x+
| 3 |
当x+
| 3 |
| 3 |
| 3 |
| 3 |
当x+
| 3 |
| 3 |
| 3 |
| 3 |
综上所述,x=5-
| 3 |
| 3 |
故答案为:5-
| 3 |
| 3 |
(2)如图,代数式|x+
| 3 |
此时,P在A、B之间,
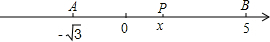
则-
| 3 |
故答案为5-
| 3 |
| 3 |
| 3 |
点评:本题考查了实数与数轴、绝对值,利用数轴,数形结合可以轻松解答.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
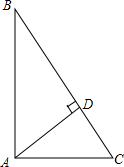 如图,在△ABC中,∠BAC=90°,AD⊥BC,AB=4,DC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,AB=4,DC=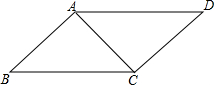 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,
如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,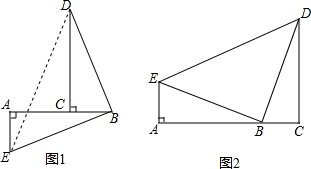 已知C点是直线AB上的一动点.
已知C点是直线AB上的一动点. 如图,在4×7的点阵中任两点竖直或水平相邻的点都相距1个单位长度,已知线段AB交线段CD于点E,试求出线段AE的长.
如图,在4×7的点阵中任两点竖直或水平相邻的点都相距1个单位长度,已知线段AB交线段CD于点E,试求出线段AE的长. 如图,在?ABCD中,点E是AD的中点,连接CE、BD相交于点F,则△DEF的周长与△BCF的周长之比C△DEF:C△BCF=
如图,在?ABCD中,点E是AD的中点,连接CE、BD相交于点F,则△DEF的周长与△BCF的周长之比C△DEF:C△BCF=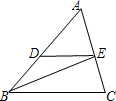 如图,在△ABC中,BD平分∠ABC,交AC于点D,过点D作BC的平分线,交AB于点E,请判断△BDE的形状,并说明理由.
如图,在△ABC中,BD平分∠ABC,交AC于点D,过点D作BC的平分线,交AB于点E,请判断△BDE的形状,并说明理由.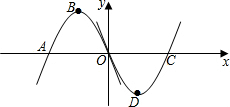 如图所示,抛物线y=ax2+bx(a<0)的图象与x轴交于A、O两点,顶点为B,将该抛物线的图象绕原点O旋转180°后,与x轴交于点C,顶点为D,若此时四边形ABCD恰好为矩形,则b的值为
如图所示,抛物线y=ax2+bx(a<0)的图象与x轴交于A、O两点,顶点为B,将该抛物线的图象绕原点O旋转180°后,与x轴交于点C,顶点为D,若此时四边形ABCD恰好为矩形,则b的值为