题目内容
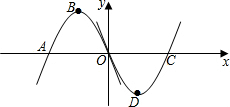如图所示，抛物线y=ax2+bx（a＜0）的图象与x轴交于A、O两点，顶点为B，将该抛物线的图象绕原点O旋转180°后，与x轴交于点C，顶点为D，若此时四边形ABCD恰好为矩形，则b的值为考点：二次函数图象与几何变换
专题：
分析：利用矩形性质得出要使平行四边形ABCD是矩形，必须满足AC=BD，即可求出．
解答：
解：如图，连接AB、OB．过点B作BE⊥x轴于点E．
要使平行四边形ABCD是矩形，必须满足AC=BD，
∴OA=OB．
∵点B是抛物线的顶点，
∴AB=OB，
∴△ABO是等边三角形，
∠BAE=60°，AE=
OA．
∵y=ax2+bx=ax（x+
）=0，y=ax2+bx=a（x-
）2-
∴A（-
，0），B（
，-
），
∴tan60°=
=
=
．
解得 b=-2
．
故答案是：-2
．
解：如图，连接AB、OB．过点B作BE⊥x轴于点E．要使平行四边形ABCD是矩形，必须满足AC=BD，
∴OA=OB．
∵点B是抛物线的顶点，
∴AB=OB，
∴△ABO是等边三角形，
∠BAE=60°，AE=
| 1 |
| 2 |
∵y=ax2+bx=ax（x+
| b |
| a |
| b |
| 2a |
| b2 |
| 4a |
∴A（-
| b |
| a |
| b |
| 2a |
| b2 |
| 4a |
∴tan60°=
| BE |
| AE |
-
| ||
-
|
| ||
| 2 |
解得 b=-2
| 3 |
故答案是：-2
| 3 |
点评：此题主要考查了二次函数图象的几何变换，根据矩形的性质和等边三角形的判定与性质得到△ABO是等边三角形是解题的难点．
练习册系列答案
小学教材完全解读系列答案
相关题目
如图，已知AO⊥OB于点O，CO⊥DO于点O，那么∠AOD+∠BOC=
如图，一轮船在海上以每小时30海里的速度向西方向航行，上午8时，在B处测得小岛A在北偏东30°方向，之后轮船继续向正西方向航行，于上午9时到达C处，这时测得小岛A在北偏东60°方向．如果轮船仍继续向正西方向航行，于上午11时到达D处，这时轮船与小岛A相距多远？