题目内容
如图，在4×7的点阵中任两点竖直或水平相邻的点都相距1个单位长度，已知线段AB交线段CD于点E，试求出线段AE的长．考点：相似三角形的判定与性质
专题：网格型
分析：延长CD至F，首先求出AB的长；由AF∥BC，得出△AEF∽△BEC，得出AE：BE=AF：BD=5：4，证出AE：AB=5：9，即可求出AE的长．
解答：解：如图所示：延长CD至格点F，
根据题意得：AF=5，BC=4，
由勾股定理得：AB=3
，
∵AF∥BC，
∴△AEF∽△BEC，
∴
=
=
，
∴
=
，
∴AE=
AB=
×3
=
．
根据题意得：AF=5，BC=4，
由勾股定理得：AB=3
| 5 |
∵AF∥BC，
∴△AEF∽△BEC，
∴
| AE |
| BE |
| AF |
| BC |
| 5 |
| 4 |
∴
| AE |
| AB |
| 5 |
| 9 |
∴AE=
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
5
| ||
| 3 |
点评：本题考查了相似三角形的判定与性质；通过作辅助线构造三角形相似，证明三角形相似是关键．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
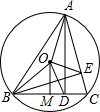如图，锐角△ABC内接于圆O，AD⊥BC，BE⊥AC，OM⊥BC，垂足分别为D、E、M．
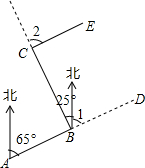林湾乡修建一条灌溉水渠，如图，水渠从A村沿北偏东65°方向到B村，从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建，可以保持与AB的方向一致？
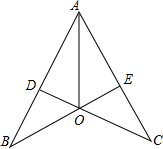如图：AB=AC，BD=CE．求证：OA平分∠BAC．
如图，数轴上的点P表示的数可能是（ ）| A、-3.7 | ||
B、
| ||
C、-
| ||
D、-
|
如图，△ABC的面积为1，分别取AC、BC两边的中点A1、B1，则四边形A1ABB1的面积为
一只自由飞行的小鸟，将随意地落在如图所示方格地面上（每个小方格都是边长相等的正方形），则小鸟落在阴影方格地面上的概率为
如图，一轮船在海上以每小时30海里的速度向西方向航行，上午8时，在B处测得小岛A在北偏东30°方向，之后轮船继续向正西方向航行，于上午9时到达C处，这时测得小岛A在北偏东60°方向．如果轮船仍继续向正西方向航行，于上午11时到达D处，这时轮船与小岛A相距多远？