题目内容
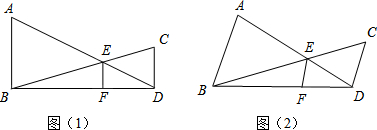
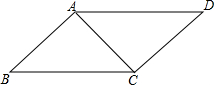 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,
如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,BC=5cm,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△ABP为等腰三角形?
考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:动点型
分析:利用AAS先证明△ABC≌△CDA,可得AD=BC,AB=CD;利用勾股定理先求得AC的长,再根据点P在BC上,点P在CD上,点P在AD上三种情况,结合等腰三角形的判定和勾股定理进行计算即可.
解答:解:在△ABC和△CDA中,
,
∴△ABC≌△CDA(AAS),
∴AD=BC,AB=CD.
在Rt△ABC中,∠BAC=90°,AC=
=
=4.
设经过ts时,△ABP为等腰三角形.当P在BC上时,
①BA=BP=3,即t=3时,△ABP为等腰三角形;
②BP=AP=
BC=
,即t=
时,△ABP为等腰三角形;
③AB=AP.过A作AE⊥BC,垂足为E,AE=
.
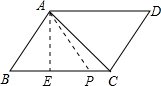
在Rt△ABE中,BE=
=
=
.
∴BP=2BE=
,即t=
时,△ABP为等腰三角形;
当P在CD上不能得出等腰三角形;
当P在AD上时,只能AB=AP=3,
∴BC+CD+DP=10,即t=10时,△ABP为等腰三角形.
答:从运动开始经过
s或3s或
s或10s时,△ABP为等腰三角形.
|
∴△ABC≌△CDA(AAS),
∴AD=BC,AB=CD.
在Rt△ABC中,∠BAC=90°,AC=
| BC2-AB2 |
| 52-32 |
设经过ts时,△ABP为等腰三角形.当P在BC上时,
①BA=BP=3,即t=3时,△ABP为等腰三角形;
②BP=AP=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
③AB=AP.过A作AE⊥BC,垂足为E,AE=
| AB•AC |
| BC |

在Rt△ABE中,BE=
| AB2-AE2 |
32-(
|
| 9 |
| 5 |
∴BP=2BE=
| 18 |
| 5 |
| 18 |
| 5 |
当P在CD上不能得出等腰三角形;
当P在AD上时,只能AB=AP=3,
∴BC+CD+DP=10,即t=10时,△ABP为等腰三角形.
答:从运动开始经过
| 5 |
| 2 |
| 18 |
| 5 |
点评:本题主要考查了全等三角形的判定与性质,等腰三角形的判定及勾股定理等知识,注意要分情况考虑问题.

练习册系列答案
相关题目
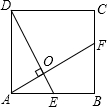 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则| AO |
| DO |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
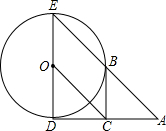 如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.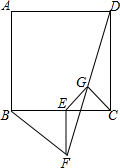 已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点E在BC上,取DF的中点G,连结EG、CG.
已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点E在BC上,取DF的中点G,连结EG、CG.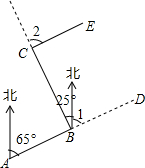 林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?
林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?