题目内容
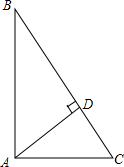 如图,在△ABC中,∠BAC=90°,AD⊥BC,AB=4,DC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,AB=4,DC=| 9 |
| 5 |
考点:解直角三角形
专题:计算题
分析:先证明△BAD∽△BCA,利用相似比得到
=
,整理得5BC2-9BC-80=0,再解方程求出BC,然后在Rt△ABC中,利用正弦的定义求sinC的值.
| 4 |
| BC |
BC-
| ||
| 4 |
解答:解:∵AD⊥BC,
∴∠ADB=90°,
∵∠ABD=∠CBA,
∴△BAD∽△BCA,
∴
=
,即
=
,
整理得5BC2-9BC-80=0,解得BC=-
(舍去)或BC=5,
在Rt△ABC中,sinC=
=
.
∴∠ADB=90°,
∵∠ABD=∠CBA,
∴△BAD∽△BCA,
∴
| AB |
| BC |
| BD |
| AB |
| 4 |
| BC |
BC-
| ||
| 4 |
整理得5BC2-9BC-80=0,解得BC=-
| 16 |
| 5 |
在Rt△ABC中,sinC=
| AB |
| BC |
| 4 |
| 5 |
点评:解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了相似的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
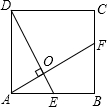 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则| AO |
| DO |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
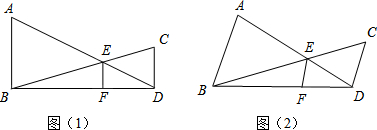
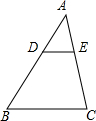 如图,DE∥BC,AD:DB=2:3,则△AED和△ABC的相似比为
如图,DE∥BC,AD:DB=2:3,则△AED和△ABC的相似比为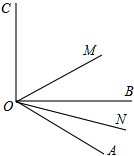 如图,已知∠AOC与∠AOB的和为180度,OM,ON分别是∠AOC、∠AOB的平分线.
如图,已知∠AOC与∠AOB的和为180度,OM,ON分别是∠AOC、∠AOB的平分线.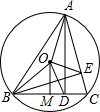 如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.
如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.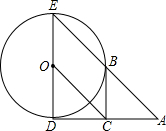 如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.