题目内容
20. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O是以BC边为直径的圆,点P为AC边上动点,⊙P的半径为2.设AP=x,则当x的取值范围是6-2$\sqrt{5}$<x≤6时,⊙P与⊙O相交.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O是以BC边为直径的圆,点P为AC边上动点,⊙P的半径为2.设AP=x,则当x的取值范围是6-2$\sqrt{5}$<x≤6时,⊙P与⊙O相交.
分析 先由勾股定理用含x的代数式表示OP,再根据两圆相交时半径与圆心距之间的关系列出不等式组,从而确定x的取值范围.
解答 解:∵∠C=90°,AC=6,BC=8,⊙P的半径为2,AP=x,
∴CP=6-x,OC=4,⊙O的半径为4;
又∵⊙P与⊙O相交,
∴$\left\{\begin{array}{l}{x≤6}\\{2<\sqrt{(6-x)^{2}+{4}^{2}}<6}\end{array}\right.$,
解得:6-2$\sqrt{5}$<x≤6.
故当6-2$\sqrt{5}$<x≤6时,⊙P与⊙O相交.
故答案为:6-2$\sqrt{5}$<x≤6.
点评 此题主要考查了圆与圆的位置关系与数量关系间的联系及不等式组的解法,利用两圆相交两半径与圆心距之间的关系是解题关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
15.某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:
则这11双鞋的尺码组成的一组数据中,众数和中位数分别是25,25.
| 尺码(cm) | 23.5 | 24 | 24.5 | 25 | 25.5 |
| 销售量(双) | 1 | 2 | 2 | 5 | 1 |
5.若A、B表示不等于0的整式,则下列各式成立的是( )
| A. | $\frac{A}{B}$=$\frac{A•M}{B•M}$ | B. | $\frac{A}{B}$=$\frac{A+M}{B+M}$ | C. | $\frac{A}{B}$=$\frac{{A}^{2}}{{B}^{2}}$ | D. | $\frac{A}{B}$=$\frac{A({x}^{2}+1)}{B({x}^{2}+1)}$ |
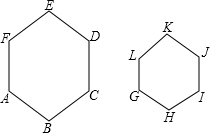 如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:
如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中: