Question

10．已知：如图1，四边形ABCD中，∠D=90°，∠B=∠C，点E在直线BC上，点F在直线CD上，且∠AEB=∠CEF．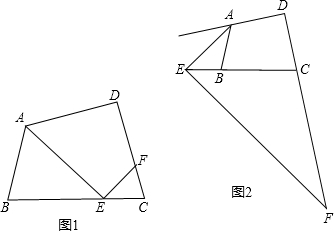

（1）若AE平分∠BAD，求证：EF⊥AE．
（2）如图2，若AE平分∠BAD的外角，其余条件不变，判断（1）中结论是否结论？并说明理由．

Answer 1

分析 （1）如图1，先根据三角形内角和定理得出∠BAE=180°-∠B-∠AEB，∠EFC=180°-∠C-∠CEF，由∠B=∠C，∠AEB=∠CEF，得到∠BAE=∠EFC，再由角平分线定义得出∠BAE=∠DAE，等量代换得到∠EFC=∠DAE．由平角的定义得出∠EFC+∠EFD=180°，那么∠DAE+∠EFD=180°，再根据四边形内角和定理求出∠AEF+∠D=360°-（∠DAE+∠EFD）=180°，进而得到∠AEF=90°，由垂直的定义证明出EF⊥AE；
（2）如图2，先根据三角形外角的性质得出∠1=∠ABC-∠AEB，∠F=∠BCD-∠CEF，由∠ABC=∠BCD，∠AEB=∠CEF，得到∠1=∠F，再由角平分线定义得出∠1=∠2，等量代换得到∠F=∠2．由平角的定义得出∠2+∠EAD=180°，那么∠F+∠EAD=180°，再根据四边形内角和定理求出∠AEF+∠D=360°-（∠F+∠EAD）=180°，进而得到∠AEF=90°，由垂直的定义得出EF⊥AE．

解答 （1）证明：如图1，∵∠BAE=180°-∠B-∠AEB，∠EFC=180°-∠C-∠CEF，
∠B=∠C，∠AEB=∠CEF，
∴∠BAE=∠EFC，
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠EFC=∠DAE．
∵∠EFC+∠EFD=180°，
∴∠DAE+∠EFD=180°，
∴∠AEF+∠D=360°-（∠DAE+∠EFD）=180°，
∵∠D=90°，
∴∠AEF=90°，
∴EF⊥AE；

（2）解：如图2，若AE平分∠BAD的外角，其余条件不变，（1）中结论没有变化．理由如下：
∵∠1=∠ABC-∠AEB，∠F=∠BCD-∠CEF，
∠ABC=∠BCD，∠AEB=∠CEF，
∴∠1=∠F，
∵AE平分∠BAD的外角，
∴∠1=∠2，
∴∠F=∠2．
∵∠2+∠EAD=180°，
∴∠F+∠EAD=180°，
∴∠AEF+∠D=360°-（∠F+∠EAD）=180°，
∵∠D=90°，
∴∠AEF=90°，
∴EF⊥AE．

点评 本题考查了多边形内角与外角，三角形、四边形内角和定理，三角形外角的性质，角平分线、垂直的定义，理清各角之间的关系，得出∠AEF+∠D=180°是解题的关键．