已知a2-6a+9与|b-1|互为相反数.求式子($\frac{1}{a+b}$+$\frac{1}{a-b}$)÷$\frac{2a}{{a}^{2}-2ab+{b}^{2}}$的值．题目和参考答案——青夏教育精英家教网—

题目内容

12．已知a²-6a+9与|b-1|互为相反数，求式子（$\frac{1}{a+b}$+$\frac{1}{a-b}$）÷$\frac{2a}{{a}^{2}-2ab+{b}^{2}}$的值．

分析根据互为相反数两数之和为0列出关系式，利用非负数的性质求出a与b的值，原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，把a与b的值代入计算即可求出值．

解答解：∵a²-6a+9+|b-1|=（a-3）²+|b-1|=0，
∴a=3，b=1，
则原式=$\frac{a-b+a+b}{（a+b）（a-b）}$•$\frac{（a-b）^{2}}{2a}$=$\frac{2a}{（a+b）（a-b）}$•$\frac{（a-b）^{2}}{2a}$=$\frac{a-b}{a+b}$=$\frac{3-1}{3+1}$=$\frac{1}{2}$．

点评此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案

每日10分钟口算心算速算天天练系列答案

3．计算：
（1）$\sqrt{81}+\root{3}{-27}+\sqrt{（-\frac{2}{3}}{）^2}$
（2）$\root{3}{8}$-$\sqrt{4}$-$\sqrt{{{（{-2}）}^2}}+|{\sqrt{2}-1}|$．

20．

如图，Rt△ABC中，∠C=90°，AC=6，BC=8，⊙O是以BC边为直径的圆，点P为AC边上动点，⊙P的半径为2．设AP=x，则当x的取值范围是6-2$\sqrt{5}$＜x≤6时，⊙P与⊙O相交．

7．下列说法中：
①一次函数y=kx+b，若k＞0，b＜0，那么它的图象过第一、二、三象限；
②函数y=-6x是一次函数，且y随着x的增大而减小；
③已知一次函数的图象与直线y=-x+1平行，且过点（8，-2），那么此一次函数的解析式为y=-x+6；
④若一次函数y=（2m-6）x+5中，y随x的增大而减小，则m的取值范围是m＞3；
正确的有（　　）

17．能确定△ABC与△A₁B₁C₁全等的是（　　）

	A．	AC=A₁C₁，BC=B₁C₁，∠B=∠B₁		B．	AC=A₁C₁，∠A=∠A₁，∠B=∠B₁
	C．	AC=B₁C₁，∠A=∠A₁，∠B=∠B₁		D．	∠A=∠A₁，∠B=∠B₁，∠C=∠C₁

4．已知一次函数y=（3+m）x+（2-m），若y随x的增大而减小，且该函数的图象与x轴的交点在原点的右侧，则m的取值范围是（　　）

1．$\frac{{\sqrt{27}×\sqrt{6}}}{{\sqrt{3}}}-\sqrt{2}$．

2．

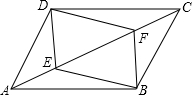已知：如图，四边形ABCD是平行四边形，DE⊥AC，BF⊥AC，垂足分别是E、F．连结BE、DF．四边形DEBF是什么特殊的四边形？请说明理由．

试题分类